DSCN0768

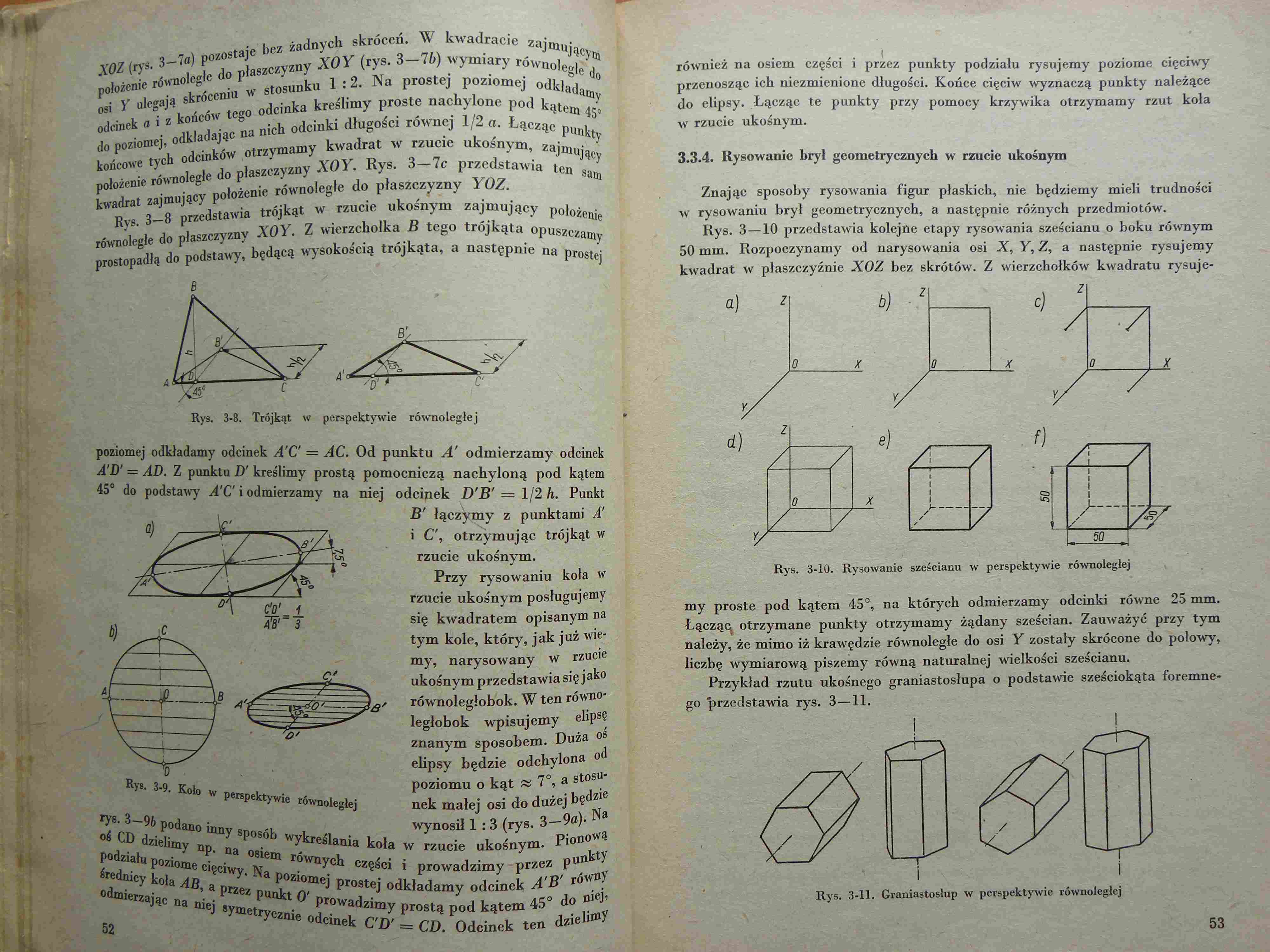
XOZ (rys. 3—7o) pozostaje bez żadnych skróceń. W kwadracie zajmującym położenie równoległe do płaszczyzny XOY (rys. 3—Ib) wymiary równoległe do osi Y ulegają skróceniu w stosunku 1:2. Na prostej poziomej odkładamy odcinek a i z końców tego odcinka kreślimy proste nachylone pod kątem 45° do poziomej, odkładając na nich odcinki długości równej 1/2 a. Łącząc punkty końcowe tych odcinków otrzymamy kwadrat w rzucie ukośnym, zajmujący położenie równoległe do płaszczyzny XOY. Rys. 3—7c przedstawia ten sam kwadrat zajmujący położenie równoległe do płasźczyzny YOZ.

Rys. 3—8 przedstawia trójkąt w rzucie ukośnym zajmujący położenie równoległe do płaszczyzny XOY. Z wierzchołka B tego trójkąta opuszczamy prostopadłą do podstawy, będącą wysokością trójkąta, a następnie na prostej

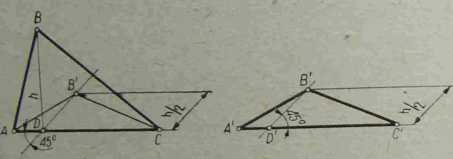
Rys. 3-8. Trójkąt w perspektywie równoległej

poziomej odkładamy odcinek A'C' = AC. Od punktu A' odmierzamy odcinek A'D' = AD. Z punktu D' kreślimy prostą pomocniczą nachyloną pod kątem 45° do podstawy A'C' i odmierzamy na niej odcipek D'B' == 1/2 h. Punkt

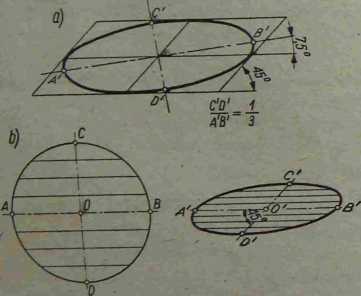
Rys. 3-9. Koło w perspektywie równoległej

B' łączymy z punktami A¹ i C\ otrzymując trójkąt w rzucie ukośnym.

Przy rysowaniu koła w rzucie ukośnym posługujemy się kwadratem opisanym na tym kole, który, jak już wiemy, narysowany w rzucie ukośnym przedstawia się jako równoległobok. W ten równo-ległobok wpisujemy elipsę znanym sposobem. Duża oś elipsy będzie odchylona od poziomu o kąt « 7°, a stosunek małej osi do dużej będzie wynosił 1:3 (rys. 3—9o); Na rys. 3—96 podano urny sposób wykreślania koła w rzucie ukośnym. Pionową oś CD dzielimy np. na osiem równych części i prowadzimy-przez punkty podziału poziome cięciwy. Na poziomej prostej odkładamy odcinek A'B' równy średnicy koła AB, a przez punkt O' prowadzimy prostą pod kątem 45° do niej, odmierzając na niej symetrycznie odcinek C'D’ = CD. Odcinek ten dzielimy

również na osiem części i przez punkty podziału rysujemy poziome cięciwy przenosząc ich niezmienione długości. Końce cięciw wyznaczą punkty należące do elipsy. Łącząc te punkty przy pomocy krzywika otrzymamy rzut koła W rzucie ukośnym.

3.3.4. Rysowanie brył geometrycznych w rzucie ukośnym

Znając sposoby rysowania figur płaskich, nie będziemy mieli trudności w rysowaniu brył geometrycznych, a następnie różnych przedmiotów.

Rys. 3—10 przedstawia kolejne etapy rysowania sześcianu,o boku równym 50 mm. Rozpoczynamy od narysowania osi X,Y,Z, a następnie rysujemy kwadrat w płaszczyźnie XOZ bez skrótów. Z wierzchołków kwadratu rysuje-

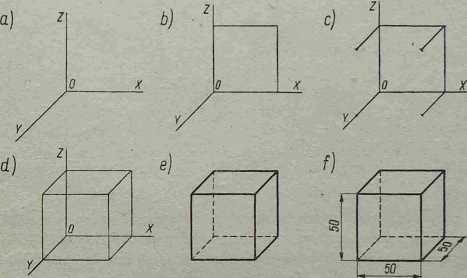
Ryś. 3-10. Rysowanie sześcianu w perspektywie równoległej

my proste pod kątem 45°, na których odmierzamy odcinki równe 25 mm. Łącząa otrzymane punkty otrzymamy żądany sześcian. Zauważyć przy tym należy, że mimo iż krawędzie równoległe do osi Y zostały skrócone do połowy, liczbę wymiarową, piszemy równą naturalnej wielkości sześcianu.

Przykład rzutu ukośnego graniastosłupa o podstawie sześciokąta foremnego przedstawia rys. 3—11.

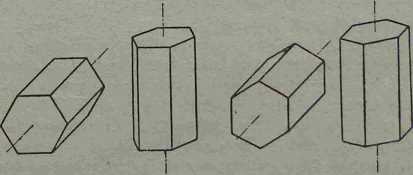
Rys. 3-11, Graniastosłup w perspektywie równoległej

53