DSCN0778

4. RZUTOWANIE PROSTOKĄTNE

4.1. ODWZOROWYWANIE PUNKTU W PRZESTRZENI

4.1.1.    Rzuty cechowane

Rzut punktu na jedną płaszczyznę dowolną (rys. 4—1) nie wyznacza położenia tego punktu względem płaszczyzny rzutów, ponieważ jest on rzutem każdego dowolnego punktu leżącego na prostej rzutującej, a jak wiemy, rzutem prostokątnym punktu na dowolną płaszczyznę nazywamy punkt przebicia ęA    jej przez prostą prostopadłą do tej płaszczyz

ny przechodzącą przez dany punkt. Tę. nie-

--oznaczoność usuniemy, jeśli obok litery^np-

\.    A\ podamy w nawiasie liczbę jednostek dłu-

o ^    \. gości odcinka AA'. Liczbę tę nazwiemy cechą'

\. punktu A, wyrażać ona będzie odległość punktu A od płaszczyzny w jednostkach Rys. 4-1. Rzut^jpunktu na jedną ^j_Ug_Q|_cj przyjętych i zaznaczonych na rysunku. Cechę 0 będą miały punkty leżące na płaszczyźnie. Punkty leżące nad płaszczyzną będą miały cechę dodatnią, np. A'(3), punkty zaś leżące pod płaszczyzną będą miały cechę ujemną, np. B'[—5). Metoda opisana wyżej nosi nazwę rzutów cechowanych, używana jest w kartografii.

4.1.2.    Rzuty punktów na dwie płaszczyzny rzutów (rzutnie)

Na rys. 4—2 przedstawiono dwa arkusze sklejki złączone ze sobą zawiasami i tak ustawione, iż jeden arkusz zajmuje położenie pionowe, a drugi poziome. W ten sposób otrzymaliśmy obraz dwu^płaszczyzn wzajemnie do siebie prostopadłych. Poziomą płaszczyznę oznaczoną będziemy dalej nazywać poziomą płaszczyzną rzutów lub rzutnią poziomą, a płaszczyznę pionową oznaczoną n% — pionową płaszczyzną rzutów lub rzutnią pionową. Krawędź przecięcia się tych rzutni oznaczymy x i nazywać będziemy osią rzutów x.

Jeśli w przestrzeni między tymi rzutniami obierzemy dowolny punkt A i poprowadzimy proste rzutujące na każdą z rzutni, to w punktach przebicia

tych prostych z rzutniami otrzymamy rzuty punktów A na rzutnię poziomą i pionową. Rzut punktu A na rzutnię poziomą oznaczać będziemy A', a na rzutnię pionową A". Rzut A' nazywamy rzutem poziomym, a rzut A" — rzutem pionowym punktu A.

% i	ł'
1
s ,x (prf I		ipi ijj
V \T»\ ‘
		V.

Rys. 4-2. Rzuty punktu na dwie rzutnie

Jeżeli rzutnię ji_z zatrzymamy w jej położeniu pionowym, a rzutnię ji_x obrócimy dokoła osi x tak, żeby zajęła położenie również pionowe (rys. 4—3), to łatwo się przekonamy, że prosta łącząca rzuty poziomy A' i pionowy A" punktu A, dalej zwana prostą odnoszącą., jest prostopadła do osi x.

Jest to dla nas bardzo ważne stwierdzenie, które zapamiętamy w następującej formie; Po spro» wadzeniu obu rzutni do jednej płaszczyzny rysunku rzuty pionowy i poziomy dowolnego punktu w przestrzeni znajdują się zawsze na jednej prostej odnoszącej prostopadłej do osi x.

Dwa punkty leżące na prostej odnoszącej .(uważając jeden za rzut poziomy, a drugi za rzut pionowy pewnego punktu) określają położenie tylko jednego punktu w przestrzeni. Postawmy

sobie teraz pytanie, czy rzeczywiście patrząc na rzuty A’ i A", przedstawione ha rysunku 4—3, jesteśmy w stanie określić położenie punktu A? Aby dać odpowiedź, obierzemy odwrotną drogę postępowania. Rzutnię n_x doprowa-

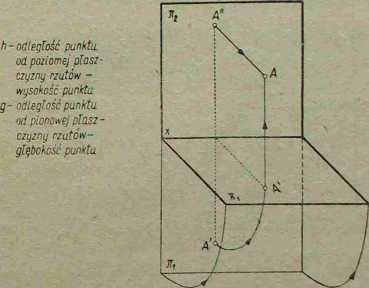
Rys. 4-4. Położenie punktu w przestrzeni wg jego rzutów

Rys. 4-3. Rzuty punktu na dwie rzutnie pionową i poziomą w płaszczyźnie rysunku

dzamy do jej pierwotnego położenia, tj. do położenia poziomego, i kolejno z punktów A' i A’’ wystawiamy proste prostopadłe do rzutni, które w przecięciu określą nam punkt A (rys. 4—4). Odległość punktu A od rzutni n_x nazywa się wysokością punktu A i jest równa odległości rzutu pionowego A” od

59