DSCN1109 (2)

2.21.    Wskazówka. Rozumowanie podobne jak w zadaniu 2.20.

2.22.    Z warunków zadania otrzymujemy układ równań:

Ja³ + ab + c — 0 (ab² + b² + c == 0.

Stąd a³ — ab² + ab — b² = 0, czyli (a — b) [a(a + b) + b] = 0. Zatem a — b = 0 lub a² + ab + b = 0.

Ponieważ a nie może być równe b, więc pozostaje

a² + ab + b = 0. Stąd b ---r i wtedy

a + 1

be C <=* [(a + 1 = 1) lub (a + 1 = — 1)].

Jeśli a + 1 = 1, to a = 0 (wbrew założeniu), zatem a 4- 1 = — 1, czyli a — — 2.

Wówczas b = 4, zaś c = 16.

Istnieje jedno równanie spełniające warunki zadania -2x² + 4x + 16 = 0.

2.23. Założenia:    Teza:

1)    f(x) = \ax² + bx + c\,    1) g:<-1; 1> - <0;3>

2) /:<-l;l>-<0;l>,

3)    g(x) = |cx² - bx + a\.

g(x) = |cx² - c + c-bx + a|^ |cx² — c| + (c + a — bx\ = = \c\-\x² - l| + |c + a — bx|.

Ponieważ

0<|x² —1|< 1 dla xe<—1;1), więc 0 < g(x) < |c| + \c + a - bx|.

Ale/(1) = la + b + c|, /(-l) = |a - b + c\,

Z założenia wynika, że/(l)e<0;l> i /(-l)e<0;l>, czyli \a + b + c| ^ 1 i |a - b + c| < 1.

Dalej mamy \a + b + c| + |a - b + c\ < 2. Zaś z drugiej strony \a + b + c + a —b + c\ < \a + b + c| + \a — b + c|

|(a + b + c) — (a — b + c)| < |a + b + c\ + |a — b + c|, czyli 2|a + c| < |a + b + c\ + \a - b + c| i 2|b| < |a + b + c\ + + \a — b + c\.

Stąd |a + c| < 1 i |b| < 1. Ponadto/(0) = \c\ < 1 i dlatego

|c + a - bx|< |a + c| + | -bx| = |a + c| + |b| |x| ^ 1 + 1 < 2. Zatem g(x) <1+2^3.

0«(x) = ax² — (a + 1) x - a, dla xeR+ u {0}

Mx) = ax² + (1 -a)x + a. dlaxei?_.

¹¹ Zbiór wartości funkcji f„ zawiera się w R ₊ u {OJ tylko wtedy,

gdy

ił R

2.24.

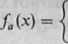
Niech

* [ax² - (a + 1) x - d] dla x > O x [ux² + (1 - a) x + a] dla x < 0.

A g_a(x) > 0,

A M*)<0.

cce R _

²⁾ Stąd wynika między innymi a > 0 i a < 0, czyli sprzeczność.

Jeżeli natomiast a — 0, to g_a{x) = — x², h_a(x) = x², więc w tym przypadku funkcja f_a nie spełnia warunku 1).

Funkcją spełniającą warunek 2) jest

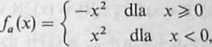
czyli/_fl(x) = -|x|x

2.25. Załóżmy, że taki wielomian istnieje i ma postać W(x) = a₀ + a_xx + a₂x² + ... + a„x\

gdzie a, e C dla i = 0,1, 2,..., n.

Wówczas mamy

a₀ + a_tp + a^² + ... + a_nf = p+ 1

a₀ + a_t (p + 2) + a₂(p + 2)² +... + a_n(p + 2)" = p.

Odejmując równania stronami otrzymujemy:

C(P + 2) - p] + a₂ [(p + 2)² - p²] +... +

+ ^fln C(p + 2)" — p"] = -1.

Ponieważ liczby (p + 2f i p* dla k = 1, 2,..., n są jednocześnie parzyste albo jednocześnie nieparzyste, więc -1 musiałaby być liczbą parzystą, co jest nieprawdą. Zatem taki wielomian nie istnieje.

2.26. Jeśli Czytelnik rozwiązał zadanie 2.25, to uzyskał również odpowiedź do zadania 2.26.

75