DSCF6585

126

Tabela 2

Wielkości charakteryzujące ruch w ośrodku lepkim

Wielkość fizyczna	Oznaczenie	Wymiar
i Opór stawiany przez ośrodek (siła Stokesa)	F,	LMT^1
i Lepkość ośrodka	1	L-'MT^l
Prędkość kulki	V	LT'
Promień kulki	r	L

W tab. | zamieszczono informacje o wielkościach określających opór ośrodka.

Nasze odczucie, mówiące o tym, że „im większe” są promień i prędkość kulki oraz lepkość ośrodka, „tym większy” opór stawiany kulce, zapiszemy w postaci zależności potęgowej:

F, = Gt]^av^f,T^e    (2a)

gdzie C jest stałą, a, b i c są nieznanymi wykładnikami, które znajdziemy stosując elementarną analizę wymiarów, tzn. wykorzystując podstawowe wymaganie, aby wielkości tworzące lewą i prawą część wyrażenia 2a miały jednakowe wymiary. Oznacza to, że jednakowe powinny być wykładniki przy symbolach długości, masy i czasu, odpowiednio po lewej i prawej stronie równania powstałego przez zastąpienie we wzorze 2 wielkości fizycznych przez ich wymiary:

LMT² = (L~ ^lMT ¹Y(ŁT^{m l})^bL^e =    (2b)

Porównanie wykładników prowadzi do układu trzech równań liniowych:

( 1 = —a+b+c    fa= 1

I i=a    m |j§|i

(-2= -a-b    (c = l

Widać więc, że siła Stokesa jest liniowo związana z prędkością, promieniem kulki i lepkością ośrodka:

F, = Cr] vr    (3)

Znalezienie wartości stałej C metodą analizy wymiarów nie jest możliwe; ograniczymy się zatem do podania gotowego wyniku: C = 6n.

1 Metoda pomiaru

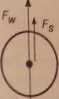
P=mg

Rys. 33. Siły działające na ciało poruszające się w ośrodku lepkim

Pomiaru współczynnika lepkości dokonujemy przez opuszczenie do badanej cieczy kulki, wykonanej z materiału o gęstości większej od gęstości cieczy i zmierzenie prędkości opadania. Ruch kulki określają dwie siły, obie niezależne od czasu - ciężar kulki P i siła wyporu F_w oraz rosnąca w miarę wzrostu prędkości siła Stokesa (rys. 33). Należy więc oczekiwać, że po osiągnięciu przez kulkę odpowiednio dużej prędkości „granicznej”, siły te zrównoważą się i dalszy ruch kulki będzie już ruchem jednostajnym.

F, = P-F„

^ 7tr³g(4 — !Jj

(4)

gdzie d_k i d_c oznaczają odpowiednio gęstość materiału, z którego wykonana jest kulka i gęstość badanej cieczy.

Po wykorzystaniu wzoru 3 mamy:

6ntj rv = ~ 7tr³(d_k — dj

czyli

(5)

2r²j(d_Ł-dJt ⁿ 91

prędkość kulki zastąpiliśmy tutaj stosunkiem drogi / do czasu jej przebycia l po to, aby we wzorze końcowym występowały wielkości bezpośrednio poddające się pomiarom. Dokładniejsze rozważania wskazują na konieczność uwzględnienia wpływu ścianek naczynia z cieczą na ruch kulki. Wpływ ten jest nieistotny tylko w przypadku, gdy rozmiary kulki są niewielkie w porównaniu z rozmiarami naczynia: r/R « 1. Ostatecznie więc współczynnik lepkości wyznaczamy ze wzoru:

n = -

2gr²t(d_k — d_e)

(6)