DSCF6594

144

(10)

i stąd

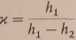
Wynik końcowy nie zależy wprawdzie od temperatury otoczenia T₀ i ciśnienia p₀, wymagane jest jednak założenie, że obie wielkości pozostają stałe w trakcie doświadczenia.

5. Opracowanie

Pomiary polegają na kilkakrotnym powtórzeniu omówionego cyklu przemian dla różnych nadwyżek ciśnienia h_t. Otrzymane ze wzoru 10 wartości | można opracować metodami stosowanymi do wyników pomiarów bezpośrednich, tzn. znajdując wartość średnią i średni błąd kwadratowy z przyjętym poziomem istotności. Zauważmy, że niedoskonała izolacja ścianek naczynia powoduje systematyczne zaniżenie wyniku, nie dokonujemy bowiem przemiany adiabatycznej opisywanej przez równanie Poissone’a (wzór 4), lecz przez równanie

pV = const.

gdzie n < | nazywa się często wykładnikiem politropy (por. rys. 39).

Z procesami adiabatycznymi mamy do czynienia np. przy rozchodzeniu się fal dźwiękowych w gazach; pomiar prędkości dźwięku pozwala więc dokładniej wyznaczyć wartość w

Pytania

1.    Zaproponować metodę pomiaru pozwalającą zmniejszyć błąd systematyczny związany z niezupełnie adiabatycznym charakterem przemian I—-II.

2.    Jaki kształt naczynia zapewnia, przy ustalonej objętości, minimalną wymianę ciepła z otoczeniem?

qj]. Pomiar ciepła topnienia lodu [27] |. Wstęp

Ciepłem topnienia nazywamy ilość ciepła potrzebną do zmiany stanu skupienia jednostki masy substancji ze stałego w ciekły.

W doświadczeniu znajdujemy ciepło topnienia lodu przy zachowaniu stałości ciśnienia w granicach ok. 3%.

2, Metoda pomiaru

Jeśli do układu złożonego z wody i lodu dostarczone zostanie ciepło 0 w ilości, która nie wystarczy do stopienia całej masy lodu, wówczas, przy zaniedbaniu strat, bilans cieplny będzie miał postać:

(1)

Q = LAm,

gdzie L oznacza ciepło topnienia lodu, Am, — masę lodu, która uległa stopneniu.

Objętość zajmowana przez lód ulegnie zmniejszeniu o AV,.

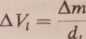
(2)

gdzie d, oznacza gęstość lodu. Woda, która powstała w procesie topnienia, zajmie objętość:

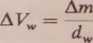
(3)

ii, oznacza gęstość wody.

Ostatecznie więc objętość mieszaniny zmaleje o AV= AV, — AF_W:

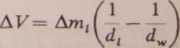
(4)