DSCN8368

^Vv

Rys. 6.3. Zdjęcie wizualizowanego przepływu

6.1.2. Obliczenie kqta natarcia ęraz składowych uderzenia i tarcia prędkości względnej

Znając wydąjność wentylatora w dowolnym punkcie charakterystyki, można ze wzoru na wydajność wirnika wyznaczyć kąt strugi napływającej do wieńca oraz kąt natarcia.

Wydąjność wentylatora wynosi

(6.6)

(6.7)

(6.8)

V=k D_l ■*,•«!• tgp_|r.V-

n

skąd obliczamy kąt strugi

7-t,

p.=arc tg—=—_r-

^r|v n • D₁ ■ 6j • «j • ą_v

Kąt natarcia wynosi

5Pi = Pl,-Pl

gdzie:    pi,. - kąt strugi gazu napływającego do wieńca,

Pi - kąt geometryczny łopatki u wlotu, ą,.    — sprawność wolumetryczną w punkcie optymalnym

jest równa 0,97.

■

Kąt natarcia 8(H zależy od strumienia objętości powietrza V przepły-_#1jącego przez wirnik. Obraz przepływu dla różnych kątów natarcia pokaźna rysunku 6.4.

V<V_n

8fli<0

V>V„

8Pl>0

RyŁ 6.4. Wektory prędkości względnych u wlotu do wieńca dla przepływu mniejszego i większego od nominalnego

Spośród różnych wartości kąta natarcia zmieniających się od wartości

ujemnych do dodatnich wyróżnia się dwie charakterystyczne, związane z nominalnym i optymalnym punktem pracy wentylatora.

W nominalnym punkcie kąt natarcia równy jest zero, zaś w optymalnym przyjmuje wartość APj.

W nominalnym punkcie pracy napływ do kanałów międzyłopatkowych jest styczny do łopatki, mówimy że jest bezuderzeniowy. W wirniku występują tylko straty tarcia.

Jeśli napływ na łopatkę nie jest styczny, wówczas w przepływie oprócz strat tarcia pojawiają się straty napływu niestycznego, zwane też stratami uderzenia. O wielkości tych strat decyduje składowa uderzenia.

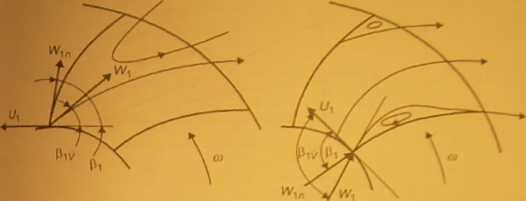
Przy napływie nieetycznym prędkość względną w_x rozkłada się. jak wynika z rysunku 6.5, na dwie składowe: jedną o kierunku równoległym do prędkości obwodowej uj., którą oznacza się jako w u, i nazywa składową straty uderzenia, oraz na składową styczną do łopatki pokrywającą się z kierunkiem prędkości wi„, którą oznacza się w\_a i nazywa składową strat tarcia.

Z trójkątów prędkości na rysunku 6.5 wynika relacja

(6.9)

w_l = u>i_a ^{+ w}lb