fizyka017

Symbolem a_t będziemy oznaczać wartość składowej stycznej wektora przyspieszenia: jest ona równa szybkości zmiany wartości prędkości

a*

de

dl

(4.7)

W szczególności dla ruchu jednostajnego po okręgu mamy a_t = 0.

Składowa normalna a_d wektora przyspieszenia (prostopadła do toru, skierowana wzdłuż promienia krzywizny), zależna od szybkości zmiany kierunku wektora prędkości, nazywa się przyspieszeniem dośrodkowym i wynosi

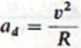
(4.8)

gdzie R promień okręgu, po którym w danej chwili porusza się punkt materialny. W ruchu po prostej wektor prędkości r ma stały kierunek, więc aj ■ 0; dla ruchu jednostajnego po okręgu v = const i przyspieszenie do-

«2

środkowe pozostaje stałe: a_d = — = const.

R

Ogólnie mamy więc

^a =    a = a_s + a_d, a = l' a? + aj    (4.9)

co ilustruje rys. 4-2. Wektor przyspieszenia a tworzy z promieniem wodzącym kąt P, przy czym tg fi = -^a1 .

O,

Kinematyka ruchu harmonicznego. Jeżeli przy wychylaniu ciała / położenia równowagi pojawia się siła wprost proporcjonalna do wartości wychylenia (względem położenia równowagi) i skierowana przeciwnie niż wychylenie, to ruch ciała jest ruchem harmonicznym. Kinematyczne równanie ruchu harmonicznego ma postać

(4.10)

gdzie x jest współrzędną określającą położenie ciała w chwili i, czyli wychyleniem ciała z położenia równowagi (początek układu współrzędnych, w którym x = 0, przyjmujemy w położeniu równowagi), przy czym -A^ x Ś.A; A jest amplitudą (maksymalnym wychyleniem), T — okresem

zywamy kąt </> =-JL f + </>«. gdzie </>₀ jest fazą początkową. Ze wzoru

(4.10) wynika, że

(4.11)

(4.12)

Ze wzorów (4.11) i (4.12) wynika, że dla maksymalnej wartości wychylenia prędkości i przyspieszenia wynoszą odpowiednio: .x„ = A, v_m = 10A, a_m = = to²A. Z tych wzorów wynika również, że faza <p pozwala określić, jaką częścią maksymalnych wartości wychylenia, prędkości i przyspieszenia są chwilowe wartości wychylenia, prędkości i przyspieszenia, to znaczy

(4.13)

x .    v    a    .

— = sin ip ,    — = cos ip .    — = —sin o

<'*

ZADANIA

4-1. Koło o promieniu R = 10 cm wiruje z prędkością kątową io = = 628 rad/s. Znaleźć czas pełnego obiegu Toraz prędkość liniową r punktu znajdującego się na obwodzie kola. Znaleźć liczbę n obrotów kola w ciągu /= 1 min.