IMGç78 (2)

Odchylenie standardowe ┼Ťrednie) zmicnncj z b─Ödziemy oznacza─ç (J - , gdzie
wska┼║nikiem jest symbol ┼Ťredniej tej zmiennej, kt├│rej dotyczy, natomiast niepewno┼Ť─ç prze
dzia┼éow─ů graniczn─ů ┬▒k
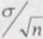
oznaczamy symbolem ┬▒6
┬▒6 jest niepewno┼Ťci─ů graniczn─ů
bezwzgl─Ödn─ů, natomiast odniesiona do v, a praktycznie do x, b─Ödzie niepewno┼Ťci─ů graniczn─ů wzgl─Ödn─ů (oznaczan─ů symbolem ff).
W tym miejscu przedyskutujemy sens liczbowej miary niepewno┼Ťci wyra┼╝onej za pomoc─ů o lub za pomoc─ů przedzia┼éu ┬▒ko. W pierwszym przypadku liczba wyra┼╝aj─ůca o jako ┼Ťredniokwadratowe odchylenie wyra┼╝a ┼Ťredni rozrzut warto┼Ťci losowych wok├│┼é warto┼Ťci oczekiwanej Liczba ta monotonicznie ro┼Ťnie, gdy rozrzut zwi─Öksza si─Ö i odwrotnie Interpretowanie tej liczbie jako pewnego przedzia┼éu ufno┼Ťci jest niepraktyczne, bo az blisko X odchyle┼ä przekracza┼éaby ┼Ťrednio granice tak obranego przedzia┼éu (patrz rys 11) Natomiast w drugim przypadku wybieraj─ůc okre┼Ťlony poziom ufno┼Ťci wyznaczamy odpowiednio du┼╝e k i odpowiedni─ů warto┼Ť─ç przedzia┼éu ┬▒ko, tak ┼╝e mo┼╝e by─ç dowolnie ma┼éo prawdopodobne (bo od nas to zale┼╝y!), aby odchylenie wykroczy┼éo poza tak utworzony przedzia┼é. Oba sposoby s─ů teoretycznie r├│wnowa┼╝ne, je┼╝eli znany jest typ rozk┼éadu (gdy nie znamy typu rozk┼éadu, to nie mo┼╝emy wyznaczy─ç przedzia┼éu ufno┼Ťci!). U┼╝ycie jednego lub drugiego sposobu rozstrzygn─Ö┼éo si─Ö w praktyce na zasadzie tradycji i u┼╝yteczno┼Ťci. Wyra┼╝anie niepewno┼Ťci za pomoc─ů odchylenia standardowego stosuje si─Ö lam. gdzie ocena niepewno┼Ťci ┼Ťluzy wy┼é─ůcznie por├│wnywaniu dok┼éadno┼Ťci do┼Ťwiadczalnych danych liczbowych. Odchylenie standardowe jest bowiem bardziej uniwersalne, nie trzeba zna─ç typu rozk┼éadu i nie trzeba dokonywa─ç arbitralnego rozstrzygni─Öcia co do wyboru poziomu ufno┼Ťci Niepewno┼Ť─ç wyniku pomiaru jest tym mniejsza, im odchylenie standardowe jest mniejsze; niepotrzebne s─ů dodatkowe komentarze, bo sens er jest jednoznaczny. Z tych powod├│w niepewno┼Ť─ç wyra┼╝on─ů za pomoc─ů odchylenia standardowego stosuje si─Ö w fizyce przy charakteryzowaniu dok┼éadno┼Ťci wyznaczenia sta┼éych fizycznych, w s┼éu┼╝bie miar przy charakteryzowaniu dok┼éadno┼Ťci wzorc├│w na najwy┼╝szym poziomie dok┼éadno┼Ťci lub te┼╝ przy charakteryzowaniu dok┼éadno┼Ťci wykonanych komparacji, np. komparacji wzorc├│w We wszystkich tych przypadkach ocena niepewno┼Ťci s┼éu┼╝y por├│wnywaniu .jako┼ŤciÔÇŁ uzyskanych wynik├│w i niczemu wi─Öcej. Sugerowanie, ┼╝e odchylenie ┼Ťredniokwadratowe ma sens jakiego┼Ť przedzia┼éu (o ma┼éym poziomie ufno┼Ťci!), jest niepotrzebne, niepraktyczne i ÔÇ×psuje" uniwersalno┼Ť─ç tej wielko┼Ťci jako miary rozrzutu - o jest uniwersalne jako ┼Ťrednie kwadratowe odchylenie, a nie jako przedzia┼é ufno┼Ťci
Natomiast niepewno┼Ť─ç wyraton─ů przedzia┼éowo' (np za pomoc─ů przedzia┼éu ufno┼Ťci) stosuje si─Ö przede wszystkim w technice, tam gdzie podejmuje si─Ö decyzje techniczne na podstawie wynik├│w pomiaru, rozstrzyga si─Ö o technicznym lub fizycznym stanie rzeczy. W├│wczas chodzi o to, czy wynik pomiaru lub wskazanie przyrz─ůdu, w takim a takim przedziale niepewne, mo┼╝e by─ç podstaw─ů uznania, ┼╝e mierzony stan fizyczny jest w┼éa┼Ťciwy -dobry czy z┼éy W┼éa┼Ťnie z tego powodu wszystkie liczbowe charakterystyki dok┼éadno┼Ťciowe u┼╝ytkowych przyrz─ůd├│w pomiarowych s─ů tworzone jako charakterystyki przedzia┼éowe, cho─ç sens podawanych przedzia┼é├│w jest zr├│┼╝nicowany Na przyk┼éad cz─Östo - upraszczaj─ůc -rozumie si─Ö niepewno┼Ť─ç wskaza┼ä przyrz─ůdu jako dopuszczalny przedzia┼é mo┼╝liwych b┼é─Öd├│w o jednostajnym rozk┼éadzie g─Östo┼Ťci prawdopodobie┼ästwa w tym przedziale Ten przedzia┼é nie jest przedzia┼éem ufno┼Ťci w tym sensie, kt├│ry zosta┼é tu zdefiniowany
Przypomnijmy, ┼╝e odrzucili┼Ťmy wcze┼Ťniej nazw─Ö ÔÇ×niepewno┼Ť─ç rozszerzona" i stosujemy nazw─Ö stosujemy nazw─Ö ÔÇ×niepewno┼Ť─ç przedzia┼éowa" W powy┼╝szym ust─Öpie jest uzasadnienie dokonanego wyboru.
Warto┼Ť─ç niepewno┼Ťci typu A otrzymujemy - jak wiemy - na zasadach statystycznych Niepewno┼Ť─ç ta jest ocen─ů skutk├│w losowo┼Ťci kolejnych wynik├│w pomiaru otrzymanych -wed┼éug naszej wiedzy - w tych samych warunkach tymi samymi przyrz─ůdami przy powtarzaniu do┼Ťwiadczenia pomiarowego w taki sam spos├│b. W wyniku otrzymujemy seri─Ö x. (o liczebno┼Ťci n) surowych wynik├│w pomiaru losowo zmiennych Losowo┼Ť─ç ta jest generowana przez specyficzne zjawiska wyst─Öpuj─ůce nieod┼é─ůcznie prawie w ka┼╝dym do┼Ťwiadczeniu pomiarowym. Jest to jakby czysty przypadek do┼Ťwiadczenia probabilistycznego M├│wi si─Ö te┼╝, ┼╝e w takiej losowej zmienno┼Ťci wynik├│w pomiaru ujawnia si─Ö obecno┼Ť─ç b┼é─Öd├│w przypadkowych.
Gdy losowa zmienno┼Ť─ç surowych wynik├│w pomiaru nie wyst─Öpuje przy powtarzaniu do┼Ťwiadczenia pomiarowego, mo┼╝e to przede wszystkim oznacza─ç, ┼╝e przyrz─ůdy s─ů ma┼éo czu┼ée albo upo┼Ťledzone jest rozr├│┼╝nianie ma┼éych zmian ich wskaza┼ä. Mo┼╝emy przekona─ç si─Ö o tym eksperymentalnie. W tym celu wywo┼éujemy ┼Ťwiadomie niewielk─ů zmian─Ö wielko┼Ťci mierzonej, jednak tak─ů, ┼╝eby otrzyma─ç daj─ůc─ů si─Ö odczyta─ç zmian─Ö wskazania przyrz─ůdu. Z takich danych mo┼╝emy obliczy─ç przedzia┼é zmian wielko┼Ťci mierzonej, kt├│rych nie dostrzegamy w danym do┼Ťwiadczeniu. Wyznaczamy w ten spos├│b przedzia┼é, kt├│ry w miernictwie nazywany jest ÔÇ×stref─ů martw─ůÔÇŁ wskaza┼ä przyrz─ůdu, a po┼éowa tego przedzia┼éu jest progiem pobudliwo┼Ťci (przyrz─ůdu). Na podstawie takich danych wyznaczamy niepewno┼Ť─ç przedzia┼éow─ů wynikaj─ůc─ů z progu pobudliwo┼Ťci, czyli ocen─Ö mo┼╝liwego rozrzutu wynik├│w, kt├│rego fizycznie nie mogli┼Ťmy stwierdzi─ç Przyjmuj─ůc rozk┼éad jednostajny w danym przedziale mo┼╝emy wyznaczy─ç odchylenie standardowe (dziel─ůc przedzia┼é przez ) z oceny przedzia┼éowej progu pobudliwo┼Ťci
Wykazuje si─Ö w statystyce, ┼╝e najlepszym przybli┼╝eniem nieznanego wyniku (na podstawie serii x, n losowych wynik├│w surowych jest ┼Ťrednia arytmetyczna (1.10) obliczona z tych wynik├│w. T─Ö ┼Ťredni─ů nazywa si─Ö w statystyce estymatorem warto┼Ťci oczekiwanej, a sen─Ö wynik├│w pomiaru nazywa si─Ö w statystyce pr├│bk─ů z populacji W naszym przypadku populacja oznacza┼éaby niesko┼äczony zbi├│r wszystkich wynik├│w, jakie mo┼╝na otrzyma─ç w danym podstawowym uk┼éadzie warunk├│w danego do┼Ťwiadczenia pomiarowego. Jest to spekulacja czysto hipotetyczna, poniewa┼╝ na uzyskanie takiej liczby wynik├│w trzeba by niesko┼äczenie d┼éugiego czasu, a utrzymanie niezmiennego uk┼éadu warunk├│w w d┼éu┼╝szym czasie jest niemo┼╝liwe. To oznacza, ┼╝e d┼éuga seria surowych wynik├│w - jak to si─Ö m├│wi w statystyce - by┼éaby statystycznie niejednorodna, czyli wyniki tworz─ůce seri─Ö nie nale┼╝a┼éyby do tego samego rozk┼éadu g─Östo┼Ťci prawdopodobie┼ästwa, bo uk┼éad warunk├│w zmienia┼éby si─Ö, a tym samym mog┼éyby si─Ö zmienia─ç v i a rozk┼éadu.
Ocen─Ö s odchylenia standardowego o charakteryzuj─ůcego rozrzut surowych wynik├│w tej serii oblicza si─Ö z (1.12), a funkcj─Ö t─Ö nazywa si─Ö w statystyce estymatorem a.
s =
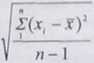
(1.12)
R├│wnolegle do rozwa┼╝a┼ä prowadz─ůcych do (1.11) wprowadza si─Ö estymator ss odchylenia standardowego ┼Ťredniej X (1.13). W obu estymatorach (1.12 i 1.13) wyst─Öpuje w
41
Wyszukiwarka
Podobne podstrony:
DSC00424 (9) yr gdzie: j ÔÇö odchylenie standardowe; y ÔÇö ┼Ťrednia arytmetyczna; y, ÔÇö stan zmiennej Y op
Kolokwium miernictwo (2) B) C) D) okre┼Ťlany Jest ┬źiwsj
68 Hygeia Public Health 2011, 46(1): 64-70 Tabela VI. Odchylenie standardowe i ┼Ť
Laboratorium Metrologii Analiza niepewno┼Ťci Odchylenie standardowe ┼Ťredniej, b─Öd─ůce miar─ů losowej
Niestety ntusimy uwzgl─Ödni─ç dopuszczalny b┼é─ůd naszych oblicze┼ä tj. odchylenie standardowe ┼Ťredniej
skanuj0004 Odchylenie standardowe ma szereg w┼éasno┼Ťci, kt├│re powoduj─ů, ┼╝e jest to miara bardzo przyd
dupa0125 Odchylenie standardowe sk┼éadnika resztowcgo, czyli ┼Ťredni blrd szacunku: (4.70) (gdzie k oz
4WZORY I OZNACZENIA p - warto┼Ť─ç ┼Ťrednia a - odchylenie standardowe n ÔÇö liczba pr├│b k ÔÇö liczba
u = gdzie: . sii si to ┼Ťrednie z pr├│b, . Si, s2 to odchylenia standardowe z populacji, . n,, n2 to l
Zdj─Öcie0702 1. Pomiar wzrostu grupy os├│b da┼é wyniki: warto┼Ť─ç ┼Ťrednia: ISO cm. odch
Zdj─Öcie1212 i 13- 2 Obliczenie warto┼Ťci ┼Ťredniej, wariancji i odchylenia standardowego N: umstn─ůbi
przedzia? ufno?ci (2) PRZEDZIA┼ü UFNO┼ÜCI. Zad.l W pr├│bie z┼éo┼╝onej z 60 danych ┼Ťrednia jest 30, a odch
wi─Öcej podobnych podstron