dupa0125

Odchylenie standardowe składnika resztowcgo, czyli średni blr\d szacunku:

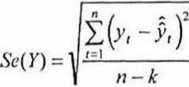
(4.70)

(gdzie k oznacza liczbę parametrów funkcji trendu lub liczbę podokresów średniej ruchomej sccntrowancj), pokaże, o ile średnio różnią się zaobserwowane wartości od oszacowanych z uwzględnieniem trendu i sezonowości.

Współczynnik zbieżności (indctcrniinacji):

<p^: =JsL

n

ŹMJ

(4.71)

i-1

pokaże, jaka część zmienności w czasie badanego zjawiska jest wywołana czynnikiem przypadkowym, gdy z kolei współczynnik determinacji

/f²= \-<f    (4.72)

określa zmienność wyjaśnioną przez trend i wahania sezonowe.

IM.20. Obliczanie składnika resztowcgo dla szeregu czasowego liczby mieszkań oddanych do użytku w tys. w kwartałach 1989-1993; wskaźniki sezonowości obliczono w IM. 19:

A,_ 11.

Kwartał	y,	1	y,	y, =y«-n^si	Mf	y, = .V„+A	M,j	(y, -yf
1 1989	23,5	1	37,04	31,19	59,08	31.46	63,34	73,96
11	35,8	2	36,52	29,73	36,89	30,76	25,41	13.69
III	29,4	3	36,00	29,30	0,01	30,24	0,70	7,29
IV	61,5	4	35,48	54,28	52,09	52.58	79,58	864,36
1 1990	23.3	5	34,96	29,44	37,65	29,38	36,96	77,44
II	28,1	6	34,44	28,03	0,00	28,68	0,34	16
III	31	7	33,92	27,61	11,49	28,16	8,07	1.21
IV	51,9	8	33,40	51,10	0,64	50,50	1,96	392,04
I 1991	23,7	9	32,88	27,68	15.88	27,30	12,96	70,56
II	29,9	10	32,36	26,34	12,67	26,60	10,89	4,84

III	28,5	11	.31.84	25,92	6,67	26,08	5.86	12,96
IV	54.4	12	31.32	47,92	41,99	48,42	35.76	497,29
1 1992	47,3	13	30,80	25,93	456,51	25.22	487,51	231,04
11	19,6	14	30,28	24,65	25,49	24,52	24,21	156,25
III	22.4	15	29,76	24,23	3,33	24,00	2,56	94,09
IV	43.7	16	29,24	44,74	1,08	46,34	6,97	134,56
1 1993	18,7	17	28.72	24,18	30,06	23,14	19.72	179,56
11	19.6	18	28,20	22,96	11,26	22,44	8.07	156,25
III	19.1	19	27,68	22,53	11,78	21.92	7,96	169
IV	30,6	20	27.16	41,56	120,06	44,26	186,6.3	2.25
Suma	642	210	642	639,32	934,63	642,00	1 025,47	3 154,64

Obliczamy miary określone w.orami (4.70), (4.71), (4.72). A. Dla sezonowości opisanej wskaźnikami względnymi:

&(>') = 1^1 = 7.21; Ve = — • 100 = 22.5%

V 18    32,1

, oij 03    ,

<? - =-— = 0,2963; R¹ = 1 - 0.2963 = 0,7037

3154.64

13. Dla sezonowości opisanej wskaźnikami absolutnymi:

7,55

= ——100 = 23.5% 32,1

1025,47

3154.64

= 0.3251; R-

= 1-0,3251=0,6749

Z porównania miar wynika, że względne wskaźniki sezonowości (A) lepiej opisuj.3 ten rodzaj wahań. Odchylenie standardowe pokazuje, że kwartalna liczba oddawanych do użytku mieszkań różni się od wielkości wyznaczanej przez, trend i względne wskaźniki sezonowości średnio o 7,21 tys. Współczynnik zbieżności wskazuje, że ok. 30% zmienności kwartalnej liczby mieszkań oddawanych do użytku w latach 1989-1993 spowodowały czynniki przypadkowe Z analizy wykresu wynika, że szczególnie duże wahania o charakterze przypadkowym wystąpiły na przelotnie 1991/92 r,

249