fiz (22)

12. POMIAR PRĘDKOŚCI DŹWIĘKU W POWIETRZU JAKO FUNKCJI TEMPERATURY

Równanie fali akustycznej

Równanie różniczkowe (nazywane równaniem falowym), opisujące propagację podłużnej fali sprężystej propagującej w kierunku osi X, ma postać:

(12.1)

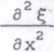
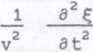
gdzie: v - prędkość rozchodzenia się fali w ośrodku, Ę -przemieszczenie wzdłuż osi X cząsteczek ośrodka, w którym fala propaguje, t - czas.

Równanie (12.1) posiada charakter ogólny i stosuje się do fal wszelkiego typu, między innymi opisuje zachowanie się dźwięku, czyli fali akustycznej w powietrzu. Prędkość podłużnej fali mechanicznej w ośrodku o gęstości p wyraża się wzorem:

v =

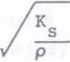
(12.2)

gdzie K_g=Kic oznacza moduł adiabatycznej ściśliwości objętościowej, *=C_p/C_v - współczynnik adiabaty, C_p oraz C_y -ciepła molowe gazu przy stałym ciśnieniu oraz przy stałej objętości, K oznacza moduł ściśliwości objętościowej występujący we wzorze (4.6).

Równocześnie prędkość fali można wyrazić poprzez jej długość A oraz częstotliwość v wzorem:

v = A v .    (12.3)

Rozwiązanie równania (12.1) nazywa się równaniem fali i może być zapisane w postaci:

C = A cos | u t - k x + <t> J ,    (12.4)

gdzie A oznacza amplitudę fali, u>=2nv - częstotliwość kołową drgań, k= 2it/A = w/i> - długość wektora falowego fali, <p -fazę początkową.

Wyznaczanie długości fali akustycznej

W przypadku fali propagującej w kierunku osi X jej faza w punkcie x^ różni się od fazy w punkcie x₂=(x₁+r) o wartość:

AS = 2n-f- lub AS = 2nv-£-    .    (12.5)

Taką różnicę faz można stosunkowo łatwo wyznaczyć, jeśli określimy    fazę fali w każdym z    tych    punktów metodą krzywych

Lissajous, obserwowanych na ekranie oscyloskopu (patrz rozdział 9 ) . Do płytek odchylania pionowego Y oscyloskopu przykładamy sygnał elektryczny generowany przez falę akustyczną w mikrofonie ustawionym w danym punkcie przestrzeni. Do płytek odchylania poziomego X przykładamy zaś sygnał pochodzący bezpośrednio z generatora pobudzającego do drgań membranę głośnika    wytwarzającego daną    falę    akustyczną.    Zmieniając

położenie    mikrofonu (a więc    x)    obserwujemy    na ekranie

oscyloskopu figurę Lissajous w postaci okręgu zmieniającego się w różnie    ustawioną elipsę bądź    nawet    w odcinek.    Odcinek ten

może być nachylony w stosunku do osi X pod kątem    n/4 lub

3 ji/4 (patrz rys. 9.1). Dwa najbliższe sobie położenia