HWScan00100

Rg cos y

2 płaskiego parabolicznego toru cząstki (krzywa kreskowana na rys. 3.14) można wnioskować, że w tym przypadku nie ma możliwości opróżnienia koła. Teoretyczna prędkość kątowa to_t ze względu na dodatkowe opory ^ruchu musi być zmniejszona współczynnikiem £ <C 1, czyli to = £ to_t. Aby parabola wysypu nakreślona pełną linią była korzystna, przyjmuje

że v_n = (0,6    0,7) uioo. Dla = 0,7, otrzymuje się £ = (0,5

do 0,6).

Wszystkie dotychczas podane zależności prędkości urabiania od pro-Wenia koła ostrzy przedstawiono na rys. 3.15 jako pęk parabol. Parabola 1 dotyczy prędkości Vioo z rys. 3.10, parabola 2 wyznacza najwyższą prędkość teoretyczną. Krzywa 3 ogranicza rzeczywisty zakres stosowalności kół komorowych.

Blhraktyczne prędkości urabiania leżą w granicach od v_n — 1,5 m/sek dla skał średnich v_n = 4,5 m/sek dla skał lekkich.

[Zakres stosowalności kół komorowych i bezkomorowych podano na . Jysunku 3.15.

jego dobrego opróżniania. Badane możliwości opróżniania naczyń z ideał, I nego urobku w kole bezkomorowym i komorowym przy różnych prę^l kościach obwodowych wskazują, że cząstka urobku nie powinna osiągną- f punktu O (rys. 3.9). W-kolc naczyniowym, w przeciwieństwie do me ; i

opróżniania z wykorzystaniem siły odśrodkowej na zewnątrz krawędzi I naczyń nie dały dotychczas jeszcze rezultatu. Przy teoretycznym rozw^ I zaniu przebiegu opróżniania przyjmuje się, że wypełnienie naczynia ukła, I da się według cylindrycznej powierzchni wysypu, której tworząca j_est I równoległa do osi koła i stanowi spiralę logarytmiczną (rys. 3.12).

3.2.6. Koło naczyniowe bezkomorowe

W kole bezkomorowym przestrzeń napełnienia naczyń powiększona jest o pierścieniową objętość na obwodzie koła. Jej wewnętrznym ograni-czeniem jest stała ściana w kształcie odcinka powłoki cylindrycznej (rys. 3.13). Zapobiega ona przedwczesnemu opróżnieniu, a zatem stracie urobku.

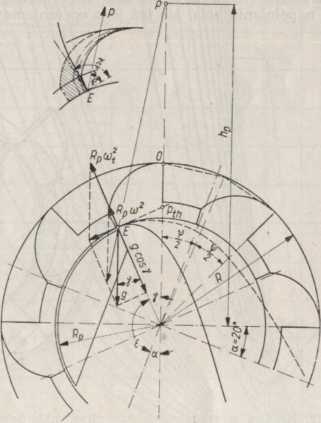
Rys. 3.14. Siły wypadkowe działające na cząstkę urobku [87]

Opróżnienie odbywa się ponad górną krawędzią tej ściany, określo^ punktem E. Najniekorzystniejszy przypadek (rys. 3.14) powstaje w naj' wyższym położeniu wysięgnika urabiającego, gdyż cylindryczna zsuwni* połączona jest sztywno z wysięgnikiem uniesionym od poziomu o kąt \\rtedy krawędź E zbliża się do punktu wierzchołkowego i jej położenie Łreślone jest kątem y. Punkt przecięcia powierzchni strugi urobku przechodzi przez punkt E. W biegunie spirali logarytmicznej (rys. 3.12) przecinają się, podobnie jak w teorii opróżniania przenośników kubełkowych, wypadkowe ciężaru własnego i siły odśrodkowej poszczególnych cząstek _urobku, niezależnie od tego, na jakim znajdują się kierunku i promieniu od osi koła.

■ Wysokość bieguna wynosi h_p =    , zatem zależy od prędkości kąto

wej koła to. Przy rosnącej prędkości kątowej biegun obniża się. Normalna do krzywej wysypu w punkcie E i linia łącząca punkt P z punktem E tworzą kąt o = arc tg // gdzie

£ o — kąt tarcia wewnętrznego urobku,

■ // — współczynnik tarcia wewnętrznego.

■Jeżeli krótka promieniowa ściana przechodząca w powłokę naczynia zbliża się do punktu E, to zmniejsza się stopniowo i ilość urobku, zakre-skowana na rys. 3.14, aż w końcu ostatnia cząstka urobku opuszcza koło w punkcie E. Największa teoretyczna prędkość kątowa to, lub prędkość urabiania v_t określona jest warunkiem równowagi siły odśrodkowej ostatniej cząstki ze składową promieniową jej ciężaru własnego

^Rp ^oy\ ⁼ '9 cos y, skąd co_f = |/ °^ ^T; _V( =j/^-

Wtprzypadku koła naczyniowego o określonej liczbie naczyń można uważać, że stosunek —■ = const, na przykład -_R^p = 0,7.

Biegun spirali logarytmicznej, który określa krzywą wysypu, leży na wysokości teoretycznej

cos y