HWScan00205

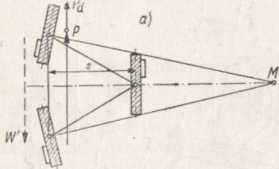
Przykłady zastosowania metody analityczno-wykreślnej. Rozważymy jako przykład niesymetryczny układ z różnymi obciążeniami poszczę-gólnych gąsienic (rys. 5.48) Gąsienice zakreskowane napędzane są z jednakową siłą. Położenie i kierunek wypadkowej siły P obu gąsienic napędzanych są znane. Nie jest natomiast znana jej wielkość. Znana jest również wielkość wypadkowej siły oporów ruchu W, która odpowiada oporom toczenia wszystkich gąsienic W = g -T Gj, oraz jej położenie i kierunek. Ponieważ momenty tarcia Mj są też nieznane, musimy wstępnie ocenić wywołane przez nie przesunięcia uoj sił W] . Przesunięcie to zgodnie z wzorem (5.93) jest mniejsze niż w_max

(5.94)

^ ^Lf* Wj < U>mMX = -4"

Siła dodatkowa W_d skierowana przeciwnie do dodatkowej siły napędowej Pj, koniecznej do jazdy po krzywiźnie, przechodzi przez punkt obrotu M, co jest niezbędne dla wywołania sił bocznych działających na środki wszystkich gąsienic. Siła ta leży na prostej łączącej ten punkt z punktem przecięcia siły P i przesuniętej siły W'. Punkt przecięcia sił W', Pd i P w przykładzie rys. 5.48 leży w nieskończoności. Wielkość P_d wynika z warunku równowagi z przesuniętym oporem W' i siłą napędową P. Siła P_d rozkłada się na trzy siły N_A, N_B, Nc. Wielkość sił N_A, N_B zależna jest od wyboru siły Nc. Według wyznaczonych sił bocznych obliczamy ej i u;; z wzorów (5.91), (5.93).

Wielkości siły N_c musimy tak długo korygować, aż trzy proste równoległe do osi poprzecznej gąsienic i przeprowadzone w odległościach e_A, e_R, e_c przetną się w przesuniętym środku obrotu M\ Ponieważ nawet duża zmiana Nc w małym stopniu oddziałuje na wielkość sił N_A> stosunkowo szybko uzyskuje się rozwiązanie. Z przesunięć w_A, w_B,

Rys. 5.49. Specjalne przypadki układu niesymetrycznego a, b — trzecia gąsienica napędzana, c, d — trzecia gąsienica nienapędzana

otrzymujemy w końcu nowe położenie przesuniętego oporu W . Jeżeli położenie to różni się od obranego poprzednio, obliczenie należy prowadzić, aż do uzyskania zgodności rozwiązań. Podczas tego wypadkowa oporu toczenia W' przesuwa się równolegle, a dodatkowa siła W</ obraca się odpowiednio wokół punktu obrotu M. Oba te ruchy odbywają się jednak

Rys. 5.50. Związki między rzeczywistym a zmniejszonym promieniem

krzywizny

a — przypadek ze zmniejszonym promieniem w układzie niesymetrycznym, b — zależność stosunku promienia rzeczywistego i zmniejszonego do wymiarów podwozia

w małym zakresie. Ponieważ uzyskiwane wartości szybko stają się zbieżne, wystarczy dwu- lub trzykrotne powtórzenie działań.

Z kolei rozważymy przypadek przedstawiony na rys. 5.49 jako jedną z czterech kombinacji, w których obie kierowane gąsienice mogą występować jako zewnętrzne lub jako wewnętrzne. Trzecia gąsienica niestero-Wana może być napędzana (rys. 5.49 a, b), albo nienapędzana (rys.

5.49 c, d). Każdy z tych przypadków ma różny stosunek , który zależy