skanuj0002 (359)

do wytwarzania podcień. W kondensatorach turbin, podnoszenia i opadania cieczy, odwadniania szybów górniczych.. ą

nJpkL

^v*it*'

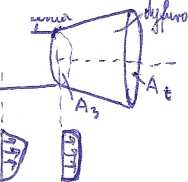
są prostopadłe. Stosunek łych wymiarów nazywany jest skalą podobieństwa liniowego

f= — = const.

¹ Im

lr-dł odcinka w obiekcie rzeczywistym lm-di. odcinka w modelu

Z warunków podobieństwa liniowego wynika podobieństwopowierzehniowe

Struga zasilająca, wpływająca przez dyszę o polu przekroju wypływającego Ae do komory mieszania wywołuje w z.wężce podciśń. poryw cząstki płynu dopływającego do komory mieszania przez przekrój o polu As. W komorze mieszania następuje połączenia obu strug w trakcie którego zachodzi wymiana energii oraz wyrówniariie prędkości ciśń., gęstość i temp.

Podobizna i analiza przepływu Podstawowe.pojęciaanalizywymiarowej.

Wartość określonej wielkości fizycznej - jest iloczynem liczby przez jednostkę miary.

w=jw> mm

{Wjwartośc liczbowa Er

[W] jednostka miary wielkości fizycznych

Hf przestrzeń wymiarowa

Wielkości w ym wzorze to wartości wymiarowe. Zbiór tych wartości wym tworzy przestrzeń wymiarową tzw II Mjrg,S,K,A Cd układ Si WAU

Wymiary wielkości podstawowej Każdą wartość w możemy zapisać

W - a* m^a kg ^bs^c

W = J3L^aM^hT^c a_yb,c,a, j3eR

Podobieństwo objętościowe

łę r.

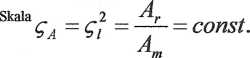
Skała

Cv    = Ci =~- = const

Spójny ukł jednostek miary to taki którego jednostki pochodne tworzą wyłącznie iloczyny potęgowe jednostek podst wielkości fizycznych bez mnożników liczbowych.

Przestrzeń Mniowa, przestrzeń wymiarowa i przestrzeń wymiarów

Element przestrzeni wymiarowej II są iloczynami liczby i jednostki miary a te są potęgami jednostek miary podstawowych wielkości fizycznych. Można powiedzieć bez precyzowania ukł jednostek miary że przestrzeń wymiarowa II stanowi zbiór elementów które są iloczynem liczby przez wymiar.

[II]- przestrzeń wymiaru

	mr	HF
1	v+w=w+v	m[w]=[w][vj
2	V+(W+Z)=(V+W i	tvj([W][ZD=([Vj[W])[ Z]
3	v+o=v
4	V+(-V>=0
5	A(V+W)=aV+aW	(ą^łiwi)^[vj^[w]^j
6	(a+b)V=aV+bV	[vf^b=m^A*wf
7	A(b*V)=(a*b)V	(ŃfFŃr
8	1*V=V	mM

Aksjomaty przestrzeni liniowej Każdy ukł n wektorów liniowo czyli w przestrzeni N albo wymiarowo w przestrzeni pi niezależnych tworzy bazę przestrzeni którą w pi nazwiemy bazą wymiarową. W przestrzeni liniowej R³ powszechnie stosowana bazę stanowią wektory jednostkowe {ijjc} w mechanice trzy wymiary {L,M,T} tworzą bazę przestrzeni wymiarów taką że [pij³.jeżeli ograniczymy się do ukł Si są to {mkg,s}

Przykład ustalić posta wzoru określającego o stratę ciś spowodowane umieszczeniem w przewodzie kryzy cBawiącęj o (kreślonej średnicy. Założono że strata dś Apszalezy od średniej pręd przepływu V przez rury jŁ ■* gęstości płynu ę Ap^s=4>(Vę)

1.    ustalamy wymiar przestrzeni wymiaru [Ap^s]=[Pa]=m¹kg¹s²()

[V]    =m‘kgVr³

[ę]    ⁼m"^cg¹s⁰}

przestrzeń trzy wymiarowa

2. maderz przekształcenia wymiarowego [Vj=mkgV¹

ję]=m³kg^Is⁰

Aisa

Ml

0,1

m

3.    ogolna postać f. wymiarowej

bllb

Stałość stosunków dł. liniowych dwóch nomologicznych odcinków np. łuków jest jednoznaczne ze spełnieniem warunków podobieństwa kształtu ponieważ kąty zawarte pomiędzy dwoma dowolnymi odpowiadającymi sobie odcinkami są również równe. Wanirkipodobieństwa kinematycznego.

W przypadku podobieństwa kinematycznego zjawisk podstawową rolę odgrywa podobieństwo pól prędkości. Znaczy to że w dwóch kinematycznych ukł. Linie prądu w przepływie rzeczywistym i modelowym są do siebie podobne i podobnie rozmieszczone w przestrzeni (pola przepływu są do siebie geometrycznie podobne) Podstawą podobieństwa kinematycznego jest skala czasu

I t_r

ę_t- — - const

Tr - czas przebiegu zjawiska w obiekcie rzeczywistym Tw -czas jprzebiegu zjawiska w obiekcie modelowym Skala podobieństw prędkości

£, = -t- = — = const

V_m 0

Skala podobieństwa strumienia objętości czyli natężenia przepływu

£,-7“

a. Cs

Na podst powyższych zależności można stwierdzić że pomiędzy polami powierzchni dwóch kinematycznie podobnych przepływów musi również zachodzić podobieństwo geometryczne.

Warunki podobieństwa dynamicznego Warunki podobieństwa dynamicznego dwóch układ obok spełnienia podobieństwo geometrycznego i kinematycznego jest zachowanie szczególnych warunków podobieństwa wszystkich sił mających wpływ na przebieg badanego zjawiska Przyjmując że ruch cieczy nieściśliwej opisuje równanie Naviera-Stokes’a zachowanie pełnego podobieństwa zjawisk modelowego i rzeczywistego wymaga spełnienia 4 kry teriów podobieństwa. Są nimi równości liczb Eulera, Frouda, Reynoldsa.

Całkowita siła działająca na cząstkę poruszającej się cieczy jest więc wypadkową następujących sil składowych:

ł) napom kryterium Eulera Eur=7Eum llbiężkości FnHFrm Sarda wewn Remem ||przyspieszenia lokalnego Str=Stm 1,2 nie rnąją wpływu na rurociąg.

Jeżeli badane zjawisko znajduje się pod przeważającym wpływem siły ciężkości wówcza posługujemy się liczbą Fronda którą możemy zapisać jako stosunek sity bezwładności do siły dężkości

y_r2 H Fr^sm

•pFconst ^)V-cons zależność Boyłea - Mariottea , £p=const—V0/T0 = V/T«gtV=V0( l+o(T-273,15)]

* ,T0 gdy temp 273,15 of=1/273,15

a współ rozszerzalności termicznej gazu H^=const pQ/T0=p/T—p=p0 [l+a(t-273,15)j Jeżeli do 1 kg gazu doprowadzi się ciepło w ilośd dq przy czym obj nie ulegnie zmianie to przyrost energii , wew gazu du wyniesie dg=du=cpłt cv-depło właściwe gazu przy stałej obj energia wewn?jest parametrem stanu i zależy ty lko od temp jeżeli proces ogrzewania zachodzi juzy stałym ciś wówczas oprócz przy rostu energii wewn zostanie wy konana praca rozprężania gdy której muszą zostać pokonane siły wywierane przez dś zew. Praca ta nazywa się pracą umieszczenia. Suma energii wew i pracy rozprężania czyli umieszczona nazywa się pojemnośdą ciepłną lub entalpią procesy dławienia się gazów dośkonałych-entalpia nie ulega zmianie.

Molowa energia wew. U i entalpia molowa gazu i są tylko funkcja temp.

KflJipP

M=C_p£sT    ^4

Cv - ciepło molowe w stałej obj. [I/$g*K] \

Cp - ciepło moowe przy stałym ciśń.

I = U^=U+RT _m ⁿ

Cp=Cp/M

Cv=Cv/M

cp,cv - ciepło właśdwe przy stałym ciśń. i obj.

próbne ciała (cząstki stale;, krople, pęcherze) są 'poddawane działaniu oporu płynu podczas takich jprocesów jak wentylacja, sedymentacja, aeracja. JDziałania wiatru na kominy fabryczne, budynki Pwzniesienia i zagłębienia terenu wytwarza określony rozkład prędkośd stref zawirowań co xna decydujący wpływ na rozprzestrzenianie się zanieczyszczeń w , ałmoderze.

Opór tarcia iopór ciś    s.

Opór profiowy Rx jest sumą opru tarcia i ooru ciś Rx=Rxt+Rxc

równe ). Ciś statyczne przyjmuje się jako nadciś p-ł-łub podciś p-

2

fdr gdm

W przepływach deczy gra podst rolę liczba Re

„ Vrdr Vmdm

Re _m— m -i

ym

siłiłabezw dno śno

#/-

si łiłalepk ci

ę*

ęg

= nA_3x2=2=>{lVUę]}^baza

Fr =

-Re «=

ęS

Rxt=cxtA

ęV²

cxt-wsp oporu tarcia

kl,k2-są praktycznie niezależne od pręd wiatru oraz skali budynku i mogą być określone dla danego modelu bud w tunelu aerodynamicznym.

W wyniku opływu terenu i bud przez wiatr tworzy się warstwa przyścienna o dużym gradiencie pręd przy pow ziemi. Parametry tej warstwy takie jak gradient pręd oraz jej grubość mają istotny wpływ na rozkład ciś na ściankach bud.

Rxc=cxcA

cxc-wspoł oporu dś

i

Rxt = b j\dx

o

b-szer

1-dł

ł-naprężenia styczne na ścianie x-odleglość od początkowej krawędzi płyty lamirama warstwa przy śdenna (rxt)łam=0,332b

^^1-^=0,6646^^

im

(Rxt)lam=    -wzór Blasiusa

(.Rxt)lam    1,328

Au = C_VAT

M = c_pAT

V-

i = u+R'T^V+A

ę

^-<v=r:

WpćLizimtrepowyK l^Cf^^cp/cv *

Wykładnik ten w umiarkowanych temp. Jest wielkością stałą i dla gazów jednoatomowych wynosi 1,62 ss K natomiast dla gazów dwuatomowych (Oz,N) wynosi 1,4 W niższych temp. Wykładnik ten jest malejącą funkcją temp.

M=£yiMi

yi - ułamek molowy składnika i w mieszaninie gazów Mi - masa molowa składnika i

Gazy raeezywłste^

Przy dśń. zbliżonym do dśń atmosferycznego oraz w temp. Znacznie przekraczającej temp. Krytyczną można w obliczeniach tech.

uznać, że równanie spełnia równanie Cłapeyrona obowiązujące dla gazów doskonałych. Jednak wraz ze wzrostem dśń. oraz obniżeniem temp. Mogą wystąpić znaczne odchylenia prawa gazów doskonałych. Równanie wirtałne- są 2 podstawowe równania uwzględmające współ, ściśliwości.

Odchylenia od gazu doskonałego zapisane są w formie wielomianu    jj / J

pv B C + ^u*™M*^a*“

nE⁼¹ v⁺r^t*~‘ 'Hf*'-

pv

nRT

= 1+B'p+C'p² -

B,C,B’,C’ - współ, wirialne zależne od rodzaju gazu i są funkcją

Równanie van dser Waalsa

(P +

~)( V - b) m nRT

dła płyty

A=a*b -paw płyty

Rei-liczba Reynoldsa odniesiona do dł płyty Ref= Vx>L

Turbułentna warstwa przyścienna.

Wosm

(cxt)turb =

VRe7

Wartość współ tarcia Cxt dla turbulentnej warstwy przyściennej są znacznie większe niż dla warstwy łaminamej

Opór dś wynika z niesymetrycznego rozkładu dś na pow opływanego dała.

Niesymetryczny rozkład dś jest spowodowany oderwaniem warstwy przyśdennej i powstawaniem obszaru zawirowań za opływanym ciałem. Opór ciś występuje nawet przy braki oderwania ponieważ rozkład dś daje składową sił skierowaną przedwnie do wektora pręd przepływu niezakłóconego Voo Przyczyną oderwania nie jest zahamowanie przepływu w warstwie przyśdennej z powodu dodatniego gradientu dś lecz nieciągłość pow opływowej czyli ostra krawędź, pow płyty.

€

1//13

Ap^s=QV°Y

4.macierz

-1		1-3
1	=	0,1
2		-1,0

b,

5.obliczamy bł ib2 -l=bl-3b2 l=b2—b2=l -2=-bl—bl=a d.podstawianrfdowzoru

Ap’=©fV

F²-f

4p

Teoria podobieństwa

'Konieczne jest zachowanie podobieństwa wartości wielkośd obserwowanych w modelu do wartości wielkośd występujących w obiekcie rzeczywistym. Znajomość kryterium podobieństwa z których wyznacza się skalę podobieństwa zjawisk w modelu do oryginału. Do spełnienia warunków podobieństwa mechanicznego oprócz zachowania podobieństwa geometrycznego modelu do obiektu rzeczywistego konieczne jest osiągnięde podobieństwa pól prędkośd czyli zachowania podobieństwa kinematycznego oraz podobieństwa układu sił czyli zachowania podobieństwa dynamicznego.

Warunki poddiieństwa wynparów i kształtów modelu do obiektu rzeczywistego,    .

Dwa układy są do siebie geometrycznie podobne gdy dowolnie wybrane odpowiadające sobie układy liniowe

ź_g =^l=> Źt^m i J

W przypadku gdy prowadzimy badania modelowe na obiekcie w którym cirózneł nie możemy posługiwać się płynem rzeczywistym. Dobranie odpowiedniej deczy modelowej jest bandor trudne a czasami niemożliwe. Decy dując się z konieczności na ciecz rzeczywistą ekspery menty należy prowadzić w odpowiednio dobranym szerokim zakresie wartośd liczby krytycznej Re na modelach o możliwie dużych rozmiarach liniowych.

Gaz doskonały _; ,

Jest to hipotetyczny model gazu w którym nie występują żadne oddziały wa rua między cząsteczko we a cząsteczki zajmują pomijalnie małą część ob jętości układu.

Równanie cłapey rona pV=nRT

R-uniwersalna siała gazowa 8134,3 jj/moł*Kj n-liczba kiłoinoli w ukł p-ciś [Pa]

V-obj [m3]

T-temp [K]

pV = -Art_m[kg/kmol\

M

m

^ę=F

; m

R -indywidualiw stała gazowa p/ę=R’T

R-dla pow 287 j/kgK Podstawowe prawo gazu

A,b - uwzględniają odchylenia gazu rzeczywistego od gazu doskonałego

Występują w gazie rzeczywistym siły przyciągające międzycząsteczkowego powodują pozorny wzrost dśń. W stosunku do ciśń gazu doskonałego i są uwzględnione przez stałą a, obj. cząsteczek gazu uwzględnia stała b

Najbardziej popularnym opisem dla gazów rzeczywistych jest równanie gazu rzeczywistego pV=mzRT

z- współ śdśliwośd gazu, załezy od rodzaju gazu oraz od temp. i dśń.

Możliwe jest jednak dokonanie pewnych uogólnień na podstawie

Zasady stanów opowiadających sobie. Zasada ta głosi, że różne zw. chem. znajdują się w stanach odpowiadających sobie icłi parametry zredukowane tzw. Temp. zredukowana(Tr), ciśnienie (pr) i obj. Zredukowana (Vr) mają takie same wartośd. Poszczególne parametry zredukowane zdefiniowane SA jako stosunek danej wielkośd do wielkośd w stanie krytycznym.

T_r=T/Tk pr=p/pk, Vi=V/Vk

Tk,pk, Vk - temp. ciśń, obj. krytyczna w stanie

krytycznym.

Jeżeli mamy do czynienia z mieszaninami gazowymi i w tym wypadku nie korzystną z parametrów krytycznych tylko z parametrów pseudokrytycznych dla mieszaniny

T

Tr=m

D-pkt oderwania A-pkt spiętrzenia Górna część rys rozkład sił.

A-w pkt A następuje spadek dś(z nadciś) do dś w pkt B(normalnego) aż do osiągnięcia podciś w pkt C, za płytąjest stałe podciś jest stałe i w przybliżeniu równa podciś w pktC.

Opór dś nie daje się wyznaczyć za pomocą teoretycznych rozważań. Można go wyznaczyć jako różnicę profilu oporu.

^ Relacja pomiędzy oporem tarda a oporem dś łub udział tych składowych w oporze profilowym zależa przede wszystkim od kształlu ciała.

Z tego względu dała które są opływane przez płyn podzielić możnanardała nieprofilowane, ciała dobrze oprofilowane (opływowe)

Można tą kł:

-dała o płaskiej ścianie czołowej -dała zaokrąglone -dała opływowe

mi

hyiTki

pr =-

tyiPu

Tki, PM - temp. i ćiśń. Krytyczne DpływciaF

^Ppdczas opływu przez wiatr budynków i innych przeszków terenowych powstaje określony rozkład prędkości, który prowadzi do rozkładu dśń. czyli poddeń. I nadciśń. na pow. Czyli do działania sił aerodynamicznych na tą pow.

W pewnej odłegłośd od budynku I ciś całkowite jest sumą dś dynamicznego i atm Powietrze które zderza się z bud zmienia kierunek i traci pręd.

Ciś przy nawietrznej stronie bud

ęV ²

*=£1^-+pa 2

KI-współ który określa jaka częśc dś dynamicznego zamieniła się na dś statyczne W przekroju II pręd pow zwiększa się w takim stopniu w jakim zmniejsza się pow przekroju poprzecznego płynącego pow. W strefie U tworzy się strefa oderwań i zawirowań dś całk na drodze I-II nieznacznie maleje na skutek strat energii natomiast dś dynamiczne znacznie rośnie wobec czego następuje spadek ciś statycznego poniżej dś atm W przekroju III który położony jest w nieznacznej odl za bud stan przepływu powraca do stanu początkowego a linie prądu mają znowu kierunek poziomy. Na zawietrznej stronie ciś jest dużo niższe od ciś atm i następują zawierowania i powstają prądy wsteczne.

Fodobny obraz przepływu wokół bud występuje pnzy rozważamu widoku z góiy. Sdaity boczne równoległe do kierunku przepływu tez znajdują się w obszarze zawirowań gdzie ciś statyczne jest mniejsze od ciś atm

P=pa-ka ? oo

2

K2-wspól określający jaka cząśc dś statycznego zamieniła sią na dś dyn związane ze wzrostem pręd wiatru.

W zast praktycznych operuje się nie ciś bezwzględnym lecz ciś względnym względem dś atm które stanowi stan odniesienia i przyjmuje się je jako