3582324682

Pytania na egzamin ustny z przedmiotu „Mechanika i ciepło” dla 1 sem. Fizyki Technicznej

1.    Wymień podstawowe wielkości fizyczne i ich jednostki w układzie SI. Wykaż, że jednostki siły i momentu pędu są odpowiednimi kombinacjami jednostek wybranych wielkości podstawowych

2.    Wskaż, stosując rachunek różniczkowy, na przyczynę występowania przyspieszenia w ruchu jednostajnym po okręgu.

3.    Pokaż, że rozumiesz sens iloczynu skalarnego i wektorowego dwóch wektorów na przykładzie momentu siły i pracy. Dokonaj prostej analizy tych iloczynów.

4.    W fizyce Arystotelesa (czyli wiele wieków przed Newtonem) sądzono, że przyczyną każdego ruchu jest działanie siły. Czy ten pogląd jest ciągle zasadny? Jaka jest Twoim zdaniem relacja między siłą a ruchem?

5.    Na rysunkach (a) i (b) przedstawiono odpowiednio zależności: v = f(t) i a = f(t). Czemu równają się pola zaznaczone na obu rysunkach?

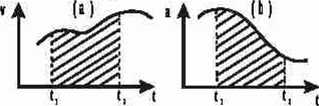
6.    Zaproponuj proste doświadczenie, w którym można wykazać, że ciała o różnych masach i kształtach spadając swobodnie z pewnej wysokości, poruszają się z tym samym przyspieszeniem

7.    Wewnątrz szklanej, obustronnie zamkniętej i wypełnionej olejem rury znajduje się pewne ciało. Rura jest ustawiona pionowo a ciało pływa u jej wierzchołka. Po odwróceniu rury o 180 stopni obserwujemy ruch ciała ku górze. Z doświadczenia wiadomo, że od pewnego poziomu ruch ten staje się jednostajny. Opisz relacje pomiędzy działającymi na dało siłami poniżej i powyżej tego poziomu,

8.    Podaj pierwsze i drugie prawo Newtona i skomentuj wzajemne relacje między nimi.

9.    Trzecie prawo Newtona. Wyjaśnij dlaczego zwykle układ „koń-wóz” porusza się w stronę, w którą ciągnie koń — mimo, że w każdej chwili koń działa na wóz z taką samą siłą jaką wóz działa na konia.

10.    Co to znaczy „rozwiązać równanie ruchu Newtona"? Podaj przykład.

11.    Omów reguły transformacyjne Galileusza opisujące położenie i prędkość punktu z dwóch inercyjnych układów odniesienia poruszających się ze względną prędkością (wzajemną) V_u.

12.    Podaj zasadę niezmienności Galileusza i wykaż jej słuszność w odniesieniu do II-go prawa Newtona.

13.    Rozważając inercyjny układ odniesienia (x, y, z) i nieinercyjny układ (x',y^J,z'), wyprowadź wyrażenie na siłę bezwładnośd.

1