3582473010

t^ań/kompas

Matematyka. Poznać, zrozumieć. Kształcenie w zakresie poditawowym

Klasa 1 • Liceum I technikum

Sprawdzian 9    Grupa A

Imię i nazwisko    _____________ Klasa    Ocena

Numer zadania	1	2	3	4	5	6	7	8	9	10	11	Suma punktów
Liczba punktów

Zadanie 1. (0-1)

Wskaż poprawne dokończenie zdania.

Przekątna AC prostokąta ABCD ma długość 6 cm i tworzy z dłuższym bokiem AB kąt a taki, że sina = y. Krótszy bok lego prostokąta ma długość

□ A. 3 cm    (UB. 2 cm    DC. /3 cm    OD. /2 cm

Zadanie 2. (0-1)

Wskaż poprawne dokończenie zdania.

Punkty A = (2, 0) i B = (5, 0) są wierzchołkami trójkąta równobocznego ABC. Wierzchołek C jest położony w I ćwiartce układu współrzędnych. Współczynnik kierunkowy prostej AC jest równy

□ A. 3    □ B. yy*    DC. &    □ D.2

Zadanie 3. (0-1)

Wskaż poprawne dokończenie zdania.

Jeśli a - 150*, to

□ A. sina = cos60* (UB. sina = cosa DC. sina=~tga □ D. cosa =-sin30*

Zadanie 4. (0-1)

Wskaż poprawne dokończenie zdania.

Dany jest trójkąt prostokątny o kącie ostrym a takim, że sina = y. Sinus drugiego kąta ostrego tego trójkąta jest równy

□ A. y    OB.^r-    □ C. -*y-    □ D. -^!y-

Zadanie 5. (0-1)

Wskaż poprawne dokończenie zdania.

Jeśli cosa =-7 i 0' < a < 180*, to sina jest równy

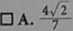
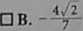
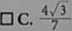
□ D.

/7

Zadanie 6. (0-1)

Wskaż poprawne dokończenie zdania.

W trójkącie równoramiennym ramię ma długość 5 cm, a podstawa ma długość 6 cm. Tangens kąta ostrego przy podstawie trójkąta jest równy

□ A.}    □ B. 3    DC.y    DD.4

O Copyright by Wydawnictwa Szkolne I Pedagogiczne jp. z o.o. Sprawdzian 9 Grupa A I 1