3582493210

Resta :

a - b=(a₁

^ |a — &| ⁼~J(^ai ~0_l)²+(^a2 ~    )²

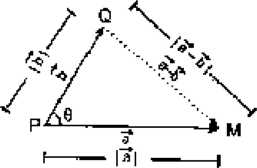
En el rectangulo sus diagonales tienen igual longitud ,entonces:

.    .    .    .    .    .<j    .    .<j

|o+ &|⁼|a- &| => |o+ 6| ^_|a-6|

Luego :

(cti+bi)² + (a₂+ b₂)² - (cti - bi)² - (0,2 - b2)²=0 => 4a₁b_l + 4a₂b₂ = 0

cipi + a₂b₂ = 0

a x a =0

ax b |a||&|

COS 9-

Por defmición del producto escalar.

a x b=a₁b₁ +a₂b₂ ....(2)

Luego: de (1) y (2): \g_Xb=o\

zrecuerbez

Si (los uectores a y b son orfogonales, enłonces el producto escalar es cero, osi: a 16=0

ORTOGONAL BE UNVECTOR 2

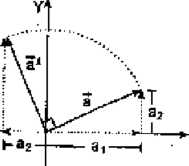
Para cada vector a=(a₁;a₂) se define su

correspondiente vector ortogonal denotado por ci~ cuyas componentes son (-a₂; a₁), es decir:

a^Ł=(-a₂; a₁)-

Graficamenteel vector a~seobtienehadendogirar el

vector a sobre su punto inidal un angulo cuya medida es 90° en sentido antihorario.

I

^ai

En la figura:

a=(a₁; a₂) a^L=(-a₂; a₁)

Luego

En el APQM: Por Ley de Cosenos

la - bf = \af + |fi|² - -2 |a||&|^eosd Despejando Cos 9: _

ABEABE im Ki4UO\ PARAM,ĘfcOGRAMECA.

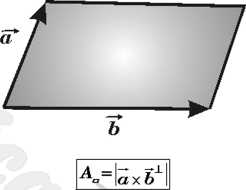
El area de una region peralelogramica cuyos lados

tienen por longitud el módulo de los vectores a y b esta dado por:

PROPIEDADES :

1)    Dados los vectores: a=(a₁; a₂ ) y 0= (b₁; b₂ ):a x 6=6 x a

2)    Va= (ai; a₂ ):ci x a= |^|²

3)    Si: a=b=> axc=bxc,VaeM²

4) \/a,b, ceM² : ax(g₊e)=ax6+axc ZRECUERBE QUE 2

Dado el vector no nulo a=(a_l; a₂); su ortogonal denotado por a , se obtiene hadendo girar a, 90⁰ en sentido antihorario, alrededor de su punto de partida; cumpliendose que :

a=(a₁; a₂)=>a^L=(-a₂; a_x)

OBSER VA CIONES:

A&GULO ENTRE EOS WECTORES

Sean los vectores a y 6 que tienen el mismo origen y forman un angulo de medida 9, luego el Cos 9 se define por:

4) a =(m; n)

²> te¹)¹—**

a=(n; - m)

3) a x =0