3582428259

6.3. Mimośrodowe ściskanie prętów smukłych

Rozważania art. 6.2 oparte były na założeniu, że przy zginaniu z udziałem sił wzdłużnych można stosować zasadę superpozycji. Jak udowodnimy poniżej, założenie to jest słuszne, jeśli odkształcenia: wywołane tym obciążeniem są pomijalnc, czyli że można stosować

regułę wymiarów początkowych (art. 1.3). Inna jest sytuacja przy mimośrodowym ściskaniu pręta smukłego (rys. 6.17), gdyż ugięcie w, aczkolwiek małe, może być rzędu mimośrodu e_x. W tym przypadku musimy rozwiązać zagadnienie uwzględniając ugięcie pręta. Dla od-

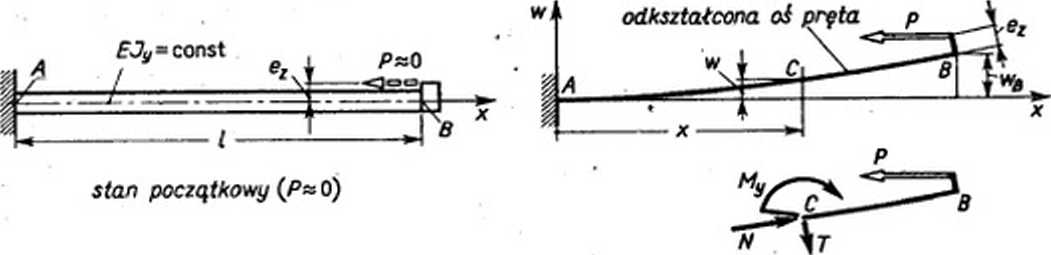
Rys. 6.17. Analiza mimośrodowego ściskania pręta smukłego

dzielonego myślowo odcinka BC z równania równowagi momentów otrzymujemy⁰ >

M, *= P(e_x + w_B-H').    (a)

Jak widać, moment ten jest funkcją e_x i nie znanego na razie ugięcia h>(x), oraz nie znanego też h»_b =* (w)*-*. Z drugiej stropy wiemy, że w stanic równowagi, w którym przecież pręt się znajduje, dla każdej współrzędnej x jest spełniona zależność. (5.20)

(b) (6.11)

(6.12)

(c)

h" = M_y/EJ,_t

która po podstawieniu wyrażenia (a) przybiera postać

* w" + k\w - ki(e_x + w_B), gdzie czynnik k, (miano cm^-1) określony jest jako

Łatwo sprawdzić, że rozwiązanie równania różniczkowego (6.11) jest

w = C, sinfc_yx + Ć₂ cosk,x + e_t + w_B

i zawiera stałe całkowania C, i C₂ oraz nie znaną wartość w_B. Wszystkie te wielkości wyznaczymy z trzech warunków brzegowych

w_x-o - 0,    (dn’/dx),-₀ = 0.    (*0*-! = ^w» •

I    •

I tak z dwóch pierwszych wynika

C₂ — — (e_t + Wa), Ci >= 0, a z trzeciego po podstawieniu powyższych wartości

H’a = (e,/cos ky /)—«*..    (^d)

^<l> Ramię siły P względem punktu B jest e, cos 0*. Gdy ugięćia są małe, wówczas cos O, różni się od jedności o małą wyższego rzędu i dlatego w równaniu (a) zamiast e, cos jest