1109145097

1.16

1.14

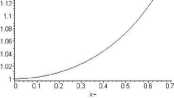
Rys. 5: Odchylenie od jedności (współczynnik x) we wzorze na okres wahadła

W przypadku małych wychyleń |0_O| ^ 1 można całkę eliptyczną łatwo obliczyć

((i -*V) (i - tr*)»(i - ir*))

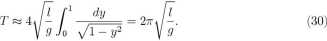
tzn. x — 1 • Ten wynik jest znany z elementarnych rozważań fizycznych.

Zwróćmy jeszcze uwagę na fakt, że okres drgań jest odwrotnością częstości kołowej drgań u = 2ir/T. Ten fakt był prawdopodobnie wykorzystywany do niezwykłe dokładnego określenia jednostki długości już w czasach poprzedzających wprowadzenie przez człowieka pisma, a więc 6-7 tysięcy lat temu! Słynne konstrukcje Stonehenge służyły prawdopodobnie do pomiaru czasu w oparciu o ruch planety Wenus, a ten z kolei określał jednostkę długości - jard megalityczny przy pomocy długości wahadła.

1.5 Dynamika bryły sztywnej

Na zakończenie uwag wstępnych przypomnimy krótko podstawowe pojęcia dynamiki bryły sztywnej. Bryłą sztywną nazywamy układ punktów, których odległości w czasie ruchu nie ulegają zmianie, tzn. dla dwóch dowolnie wybranych punktów ri, r2, |ri — ro| — const. Jeśli przez p oznaczymy gęstość masy bryły, to położenie środka masy ro jest określone związkiem

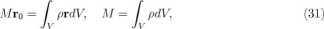
gdzie całkowanie jest rozciągnięte na całą bryłę V. Ruch punktów bryły sztywnej r (t) można opisać jako superpozycję ruchu postępowego środka masy ro (t), który spełnia równania Newtona

M r₀ = P.    (32)

gdzie P jest całkowitą siłą zewnętrzną, działającą na bryłę, oraz tak zwanego ruchu kulistego wokół osi chwilowego obrotu, przechodzącej przez środek masy. Z uwagi na warunek sztywności bryły, który można napisać w postaci

(r - r₀) ■ (r - r₀) = const => (r - r₀) • v =0, v := r - r₀,    (33)

tzn. v jest prędkością ruchu względnego względem środka masy. Prędkość v można napisać w postaci

v = wx (r r₀),    (34)

11