1109145108

Ta wartość częstotliwości u> jest nazywana wartością własną. Rozpatrzmy teraz drgania tej masy wymuszone przez siłę okresową P = Po sin pt. Równanie (1) musimy zasąpić następującym

d?x

~ ~^^x + ^po sin pt.    (4)

Rozwiązanie szczególne tego równania różniczkowego jest następujące

x =

Po

k — mp²

sin pt —

'(£)-

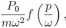
i

i-4'

(5)

Funkcja / jest przedstawiona na Rys. 01.

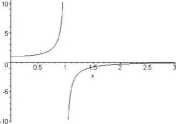
Rys. 01: Amplituda drgań wymuszonych sprężyny: x — p/ui.

Jest oczywiste, że wartość amplitudy drgań wzrasta w sposób nieograniczony, gdy wartość częstotliwości zbliża się do wartości własnej. Ten efekt nazywamy rezonansem.

Zwykle obciążenia dynamiczne nie mają prostej postaci harmonicznej, występującej w powyższym przykładzie. W wielu problemach praktycznych daje się je jednak przedstawić w postaci superpozycji wielu, czasem nieskończenie wielu, funkcji harmonicznych. Obciążenie jest wtedy charakteryzowane zbiorem wielu częstotliwości. Ten zbiór nazywamy widmem. Jeśli częstotliwość własna należy do tego zbioru to musi się pojawić zjawisko rezonansu.

Celem tych wykładów jest analiza tych problemów zarówno dla układów o skończonej, jak i o nieskończonej (tzw. układów ciągłych) ilości stopni swobody.

1.2 Dynamiczne stopnie swobody, więzy odkształcalne

Stan przemieszczenia elementów konstrukcji opisujemy w dynamice, podobnie jak w zagadnieniach statycznych, przy pomocy zbioru pewnych współrzędnych uogólnionych. Liczba niezależnych współrzędnych uogólnionych, niezbędnych do określenia chwilowej konfiguracji konstrukcji nazywa się liczbą dynamicznych stopni swobody d. Jak wiadomo z mechaniki ogólnej, punkt materialny ma w przestrzeni trzy stopnie swobody, na płaszczyźnie - dwa stopnie swobody, tarcza sztywna w ruchu płaskim ma trzy stopnie swobody, bryła sztywna w przestrzeni ma sześć stopni swobody, itd. Te elementy, wchodzące w skład modelu ustroju budowlanego są powiązane z ostoją (podpory), a między sobą - więzi-ami. Te ostatnie mogą być odkształcalne i wtedy nie zmieniają liczby dynamicznych stopni swobody, lub też nieodkształcalne, przez co nakładają na układ więzy kinematyczne. Liczba dynamicznych stopni swobody układu złożonego jest równa sumie lokalnych stopni swobody pomniejszonej o liczbę ograniczeń, wynikających z więzów.

3