1109145625

Metody numeryczne - 2. Metody dokładne rozwiązywania układów równań liniowych

2. Metody dokładne rozwiązywania układów równań liniowych

Metody rozwiązywania układów równań liniowych dzielą się na dwie grupy: metody dokładne i metody przybliżone (iteracyjne). Metody dokładne polegają na tym, że po skończonej liczbie działań arytmetycznych na współczynnikach układu równań otrzymujemy rozwiązanie tego układu. Słowo „dokładne” nie ma nic wspólnego z dokładnością uzyskanego rozwiązania, gdyż jest ono obarczone błędami wynikającymi z konieczności zaokrąglania liczb stanowiących wyniki działań pośrednich.

Metody przybliżone (iteracyjne) polegają na sekwencyjnym postępowaniu, w wyniku którego otrzymujemy rozwiązanie układu równań, z tym że w każdym kroku uzyskujemy kolejno przybliżenie szukanego rozwiązania. Metody te są procesami nieskończonymi, przerywanymi w momencie, gdy zostaje osiągnięta zadana dokładność rozwiązania. Dla metod iteracyjnych istotna jest sprawa dotycząca zbieżności ciągu kolejnych przybliżeń.

2.1. Układy równań o macierzach trójkątnych

Weźmy pod uwagę układ

GX = B

gdzie G jest macierzą trójkątną górną, czyli układ:

(2.1)

011*1 + 012*2 + - + 0111-1*71-1 + 01i>*» = *1

022*2 + - + 02»-l*n-l + 027i*n = ^b2

(2.2)

071-171-1*71-1 + 071-171*71 ^— bU-l 07171*71 = K

Zakładamy, że elementy głównej przekątnej macierzy G są różne od zera, tzn. ga ^ 0 dla i = 1,2, ...,n. Wówczas układ równań (2.2) ma dokładnie jedno rozwiązanie, bo |G| * 0. Rozwiązanie znajdujemy w sposób rekurencyjny zaczynając od ostatniego równania:

Wstawiając do równania przedostatniego mamy:

9nn

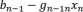
9n-m-i

i tak postępujemy kolejno.

© Uniwersytet Ekonomiczny w Krakowie 19