1060440362

pomiaru. Wariancja jest duża - gdy są duże odchylenia poszczególnych wyników od średniej, maleje - gdy odchylenia maleją do zera.

Odchylenie standardowe pojedynczego wyniku pomiarowego, będącego elementem zbiorowości generalnej, równe jest pierwiastkowi z wariancji:

2>,-*₀)²

(5.4.4)

Dla zbiorowości próbnej o malej liczebności obliczana jest przybliżona wartość (tzw. średnie odchylenie standardowe).

fe*,-*)²

(5.4.5)

Odchylenie standardowe (podobnie jak wariancja) jest miarą średniego odchylenia wyników od wartości oczekiwanej (średniej). Ma ten sam wymiar co zmienna x i jest przyjmowane jako miara przypadkowej niepewności pomiarowej. Często używa się nazwy : średni błąd kwadratowy .

Kolejnym parametrem statysty cznego rozkładu jest standardowe odchylenie średniej arytmetycznej.

Jak w iadomo, średnia arytmetyczna wyznaczona na podstawie eksperymentów jest obarczona błędem, który jest funkcją błędów pojedynczego pomiaru. Dla populacji odchylenie standardowe średniej arytmetycznej wyraża się wzorem (błąd standardowy średniej):

cr

<7

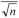
n

(5.4.6)

dla próby:

s

lice,-*)²

«(«-!)

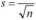
(5.4.7)

5.5. Funkcja gęstości rozkładu i prawdopodobieństwo

Jeśli rozważy' się często spotykany w laboratorium przypadek wielokrotnego pomiaru tej samej wielkości, to średnia arytmetyczna z otrzymanego w wyniku pomiarów ciągu n liczb będzie jedynie pewnym przybliżeniem wartości dokładnej tej wielkości. Rozrzut wielkości mierzonych w'okól wartości dokładnej (aproksymowanej przez średnią) wiąże się z pewną funkcją gęstości rozkładu prawdopodobieństwa p(x). Prawdopodobieństwo P, że wartość mierzona x znajdzie się w przedziale (X|, x₂), określona jest przez całkę:

P[xe(x,,x₂)]= jp(x)dx    (5.5.1)

19