3226794638

XXVII. GEOMETRIA ANALITYCZNA - PŁASKA

Geometria analityczna - jest to dział geometrii badający przestrzeń euklidesową i jej podzbiory {figury geometryczne) metodami analitycznymi (obliczeniowymi) i algebraicznymi. Badane figury są opisywane w wybranych układach współrzędnych za pomocą odpowiednich równań.

1. GŁÓWNE UKŁADY WSPÓŁRZĘDNYCH

Układ	Rysunek			Uwagi cd. patrz wektory
Kartezjański (prostokątny) na płaszczyźnie	Y ^y\ ^yK		^=UA.yA) \d =(.V«, yB)	X - oś odcięta (- «>; + oo) Y - oś rzędna (- oo; + oo) d - długość odcinka AB d = |AB| = 7(a:b - xA)^2 + 0'b - 3'a)^2
			_!_^ v
Biegunowy (polarny)	rA nk	A=(rA:(pA) Kd i h Y SA X		Ta = OA - wektor wodzący punktu A rA - promień wodzący punktu A, moduł wektora ta <pA - kąt biegunowy {współrzędna kątowa, amplituda, faza) punktu A [radj — nie jest określony dla r = 0. fO; 271) albo [a; a + 2%) albo (- oo; + oo) X - oś biegunowa {można przyjąć inną oś biegunówą) d - długość odcinka AB
	0 - biegun			d = |AB| = yjra^2 + rB^2 + 2 rA rBcos((pB - cpA)

Zamiana współrzędnych kartezjańskich na biegunowe i odwrotnie:	x = r • cos <p y = r • sin <p	y sin <p = —=== Jx^2+y^2 cos <p = —- V*^2 + y^2		(r.(p) !
		r = y]x^2 +y^2 > 0	r-cos ty

2. P RZĘSY NIECI E I OBRÓT UKŁADU WSPÓŁRZĘDNYCH

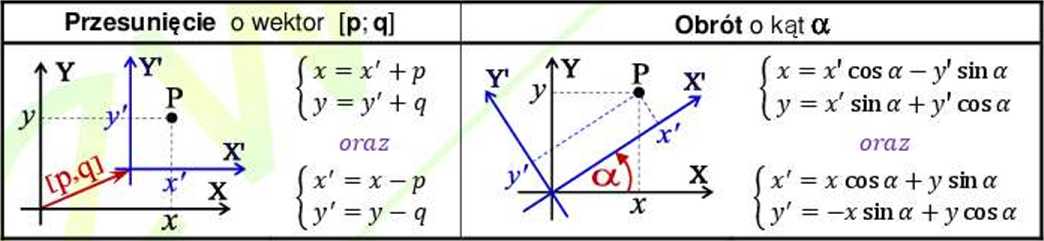
3. NAJWAŻNIEJSZE RODZAJE RÓWNAŃ KRZYWYCH

Postać równania	Wzór	Przykłady	Uwagi
Jawna ft/vspół. kartezjańskie)	y =/(*)	parabola: y = .r	najczęściej stosowana w szkołach
Jawna (współ, biegunowe)	r.\ =f(<P)	okrąg: rA = r, sp.Ar.: rA = a (p	patrz współrzędne biegunowe sp.Ar. - spirala Archi medesa
Uwikłana	F(x,y)= 0	okrąg: .v^2 + y^2 = r	np.: gdy nie da się przekształcić równania do jawnej postaci
Parametryczna	b = /2(0	. ( X = 1" cos t °^g= (y = r • sin t	współrzędne punktów należących do krzywej zależne od parametru t

© Copyright by Ewa Kędzi orczyk

- 251 -

w w w. /na tein a tyka.s osnowiec.pl