3226794648

XXVIII. GEOMETRIA ANALITYCZNA - PRZESTRZENNA

Geometria analityczna - jest to dział geometrii badający przestrzeń euklidesową i jej podzbiory {figury geometryczne) metodami analitycznymi (obliczeniowymi) i algebraicznymi. Badane figury są opisywane w wybranych układach współrzędnych za pomocą odpowiednich równań.

1. GŁÓWNE UKŁADY WSPÓŁRZĘDNYCH PRZESTRZENI

Układ

Rysunek

Uwagi

cd patrz wektory

Kartegański

(prostokątny) w przestrzeni

Z'
“B
y o
k/\
	I /

Y

—>

X. Y - odpowiednio oś odcięta, oś rzędna Z - oś prostopadła do osi X i Y

A=(.v_a ; y_A; z_A), B =(.v„; y_B; z_B) - punkty A i B Współizędne wektora AB:

AB = [x_B - x_A. y_B - y_A; z_B -z_A]=~u ~u = [u_x; Uy\ uJ Długość odcinka AB:

d = |AB| = V(x_B ~ *a)² + 0'b ~ 3'a)² + (z_B ~ ^za)²

Walcowy

(cylindryczny)

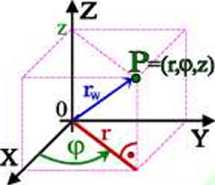
r_w = OP = [n (p; z] - wektor wodzący punktu P,

r - odlegbść od osi Z rzutu punktu P na płaszczyznę XY. <p -kąt pomiędzy dodatnią osią X a rzutem wektora OP na płaszczyznę XY

z - odległość rzutu punktu P na oś Z od punktu (0; 0; 0), J(r, <p, z) -jakobian przejścia na współrzędne walcowe.

x = r • cos <p y = r • sin q> z = z

r =

<P

z =

^*² +y^{Z >} ° y    r_K = [.x; y; z] = [rcostp; rsiii(p; z]

= arc tg- = arc sin- __ r r—--    x -i

x    r    r_w = [r, <p; z] = I yjx^z +y²; arc cos    z I

z oraz ](r,(p,z) = T    ^r

Sferyczny

(kulisty)

~F = OP = [?-, (p; d] - wektor wodzący punktu P, r - promień wodzący punktu P odległość punktu P od początku układu współrzędnych,.

(p - kąt między dodatnią półosią X a rzutem wektora OP na płaszczyznę XY. tzw. długość azymutalna 0 <<p< 2x 0 - kąt między dodatnią półosią Z a wektorem OP, tzw. odległość zenitalna 0 < 6 < x_

x = r • sin 0 • y = r • sili 0 • z = r • cos 0

cos <p sin <p

r = y]x² +y² + z² > 0

.    y/x²+y²    z

0 = arc tg-= arc cos-

z    r

<p = arc tg -

Jakobian przejścia: J(r,<p,&) = r² • sin 0

2. NAJWAŻNIEJSZE RODZAJE RÓWNAŃ POWIERZCHNI

Postać równania	Wzór		Uwagi
Jawna	z=f(x,y)		zawsze dająsię sprowadzić do równań parametrycznych lub wektorowych - ustalając parametry np. u =x, v =y
Uwikłana	F(x, y, z) = 0		stosowana często, gdy nie da się przekształcić równania do postaci jawnej
Parametryczna	◄	x = x(u, V) y = v) k Z = Z (u, v)	współrzędne punktów powierzchni zależą od parametrów (np. u, v): każda parametryzacja wyznacza pewną siatkę (u = constans, v = constans) współrzędnych krzywoliniowych na powierzchni
Wektorowa	r = r(u, v)		stanowi wektorowy zapis postaci parametrycznych

© Copyright by Ewa Kędzi orczyk

- 265 -

w w w. /no tein a tyka.s osnowiec.pl