3226794642

A. Okrąg

Okrąg - jest to zbiór wszystkich punktów płaszczyzny równo oddalonych od ustalonego punktu (zwanego środkiem okręgu).

Oznaczenia:

s = (0, 0)

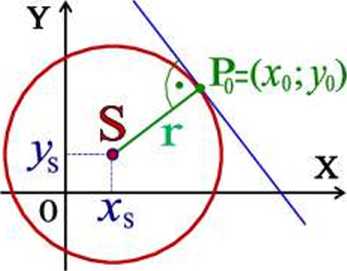
^S = (^xs->'s)

r

t

Po = (x₀,y₀)

środek (środek symetrii) okręgu,

środek układu współrzędnych,

środek okręgu po przesunięciu o wektor

[x_s,y_s], gdzie: x_s,y_s - w spód rzędne środka S,

punkt leżący na okręgu,

gdzie: XQ,yo - współrzędne punktu Po.

długość promienia okręgu: r = |SPo|,

kąt między półprostą SP₀ i dodatnią osią X,

dla punktu P₀ należącego do okręgu,

długość promienia wodzącego punktu A.

r.4

Lp.	Zagadnienia	Wzory i uwagi
(la)	Równanie kanoniczne dla S = (0,0)	X^1 Ą-y^1 = r^2
(lb)	Równanie kanoniczne dla S = (xs,ys)	(x — xs)^2 + (y — y*)^2 = r^2
(2)	Równanie ogólne (typu kołowego) dla S = (xs,ys)	X^1 + y^1 — 2xsx - 2ysy + c = 0 zal.: r^2 = xj + y^2 — c > 0 lub inaczej: Ax^2 + Ay^2 + Dx + Ey + F = 0 zal.: r^1 = —(D^2+E^2-iAF)> 0
(3a)	Równanie parametryczne dla S = (0,0)	(x = r • cos t |y = r • sin t *te[0-,2n)
(3b)	Równanie parametryczne dla S = (xs,ys)	(x = xs + r • cost [y = ys + r- smt Ate[0;2^)
(4 a)	Styczna do okręgu w punkcie Po dla S = (0,0)	XoX + y0y = r^2
(4b)	Styczna do okręgu w punkcie Po dla S = (xs,ys)	(*o - *s) 0 - xs) + (y0 - ys) (y - ys) = r^2
(5)	Warunek styczności prostej y = mx + n do okręgu (lb) dla S = (xs,ys)	( y = mx +n ({x-xs)^2 + (y-ys)^2=r^2 =» ^A = 0
(6 a)	Równanie biegunowe dla S = (rs, <ps)	rA - 2rArs cos(<pA - <ps) + r^2 = r^z
(6h)	Równanie biegunowe dla S = (0,0)	^rA = ^r	*A=!rA,tpA> rj ^>S (rsxps) j <>• V,j
(6c)	Równanie biegunowe okręgu przechodzącego przez biegun O dla 0 = (0,0), S = (rs,0) patrz współrzędne biegunowe	rA = 2r cos <pA

© Copyright by Ewa Kędzi orczyk

- 255 -

w w w. matematyk a. s os no wiec.pl