3226794645

D. Parabola

Parabola - jest to zbiór wszystkich punktów płaszczyzny równo oddalonych od danego punktu (ogniska )\ (xl danej prostej (kierownicy) nie zawierającej F.

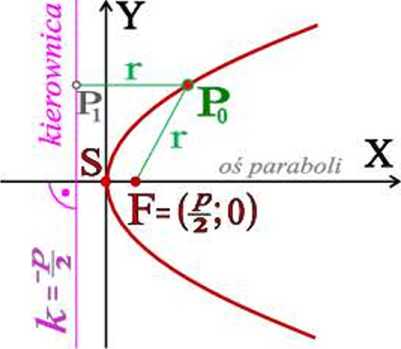
Oznaczenia:

s = (0, 0)

s = (*s,y_s)

Po=(x₀,yo)

Pi

F

P

t

n ierz.chołek paraba li,

środek układu współrzędnych,

wierz.chołek paraboli po przesunięciu

o wektor feysk

punkt leżący na paraboli,

gdzie: Xo,yo - współrzędne punktu Po,

punkt na kierownicy: PiP© 11 SF ,

ognisko paraboli: , |SF| = ^ ,

parametr ogniskowy paraboli: p > 0, kąt między pół pros tą SPo a osią X, dla punktu P₀ należącego do paraboli, ogniskowy promień wodzący paraboli:

r= |FP₀| = |P,P„I = | x-x_s +| |. promień wodzący punktu A na paraboli (układ biegunowy), A = (i'a> ^a)-

Lp.	Zagadnienia	Wzory i uwagi
(la)	Równanie kanoniczne dla S = (0,0)	y^2 =2px albo X^2 = 2py dla p > 0
(lb)	Równanie kanoniczne dla S = (xs,ys)	(y-y,)^1 = Zp(_x-xs) dla p>0
(2)	Równanie ogólne (lb) dla S = (xs,ys)	y^2 - 2px - 2ysy + 2pxs + yj = 0 <=> x = a'y^2 + b'y + c‘ lub inaczej: By^2 + Dx + Ey -\- F = 0 A B * 0 Ax^l + Dx + Ey + F = 0 A A 0
(3)	Równanie parametryczne dla S = (0,0)	f^x = 2ft AteR (y = 2 pt
(4)	Styczna do paraboli (la) w punkcie Po	yyo = p(x + x0)
(5)	Warunek styczności prostej Ax + By +C =0 do paraboli (la)	pB^2=2AC
(6)	Równanie biegunowe (la) dla S = (0,0)	4acos(pA ^TA . 2 ^sm <Pa
(7)	Równanie wierzchołkowe (la)	y^2 = 2px bo £ = 1
(8)	Mimo śród	2c c £ = — = - A £ = 1 2 a a
(9)	Ognisko (lb) dla S = (x5,y5)	^F = (^xs ^+ ^> ys) albo F = (.vy, ys 4-
(10)	Kierownica dla S = (xs,ys)	. P k: x = xs-~
(U)	Oś symetrii dla S = (xs,ys)	V) II
(12)	Wierzchołek dla S = (xs,ys)	jeden: W = S = (xs; ys)

© Copyright by Iiwa Kędzi orczyk

- 258-

w w w. ma tern utyka. sosno wiec.p /