3226794644

C. Hi.p.erb.oJ.a

Hiperbola - jest to zbiór wszystkich punktów płaszczyzny, których moduł różnicy odległości od dwóch ustalonych punktów (ognisk) jest stały (/' wynosi 2a - |n - n| = | |FiPo| - IP0F211 * 0).

Oznaczeniu:

s = (0, 0)

S = (x_s,y_s)

Po = (x₀,y₀) f,,f₂

c

a, b

r\, r2

P

t

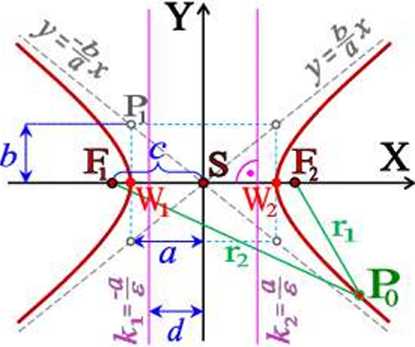
r.\, r

Środek symetrii hiperboli,

środek układu współrzędnych,

środek symetrii hiperboli po przesunięciu

o wektor [x_s,y_sJ»

punkt lezący na hiperboli,

ogniska hiperboli: |F1F2I = 2-c = 2-e •a,

odległość ognisk od środka hiperboli,

półosie hiperboli: a, b > 0.

a - półoś rzeczywista, b - pół oś urojona,

ogniskowe promienie wodzące,

parametr ogniskowy hiperboli: p = b²/ a,

kąt między półprostą SPo a osią X, dla

punktu Po należącego do hiperboli,

promień wodzący punktu A na hiperboli

(układ biegunowy), A = (r,<p) = (i’a»<Pa).

Lp.	Zagadnienia	Wzory i uwagi
(la)	Równanie kanoniczne dla S = (0,0)	x^2 y^2 y^2 x^2a^2 b^2 a^1 b^2
(lb)	Równan ie ka non iczne dla S = (xs,ys)	(*-*)* (y-y,)^2 „ a^2 b^2
(2)	Równanie ogólne dla S = (xs,ys)	b^1x^L - a V - lb^lx,x + la^ly, + b^lx\ - a^2y] - a^lb^l = 0 lub inaczej: Ax^2 + By^2 + Dx + Ey + F = 0 A AB< 0
(3)	Równanie parametryczne dla S = (xs,ys)	a ^Xs cos t A te [0; 2n) [y = ys + b-tgt
(4)	Styczna do hiperboli (lb) w punkcie Po	(*o - *j)0 - *s) (yo - y*)(y - ys)
		a^2 b^2
(5)	Warunek styczności prostej Ax + By +C =0 do hiperboli (la)	A^2a^2 — B^2b^2 — C^2 =0
(6)	Równanie biegunowe dla S = (0,0)	ab ^T~ i—-—r— Ja^2 sin' <p — b cos^2 <p
(7)	Równanie wierzchołkowe (la)	y^2 = 2px — (1 — s^2)x^2
(8)	Mimośród	2 c c ^8 2 a a ^	b^2 1 + -7 A £ > 1 a^2
(9)	Ogniska dla S = (%s,ys)	F 1,2 = (^xs + o ys) A c^2 = a^2 + b^2
(10)	Kierownice dla S = (xs,ys)	a a^2 k 12: x = xs + - = xs H--A c =£ 0 £ C
(11)	Asymptoty dla S = (0,0)	b hi- y = +
(12)	Wierzchołki dla S = (xs,ys)	dwa: WL2 = (xs + a; ys)

© Copyright by Ewa Kędzi orczyk

- 257 -

w w w. matematyk a. s os no wiec.pl