3833473523

Diagnostyka’27 - Artykuły główne JASTRIBOW. GAD, SŁOŃ, Analiza komputerowa diagnozowania defektów...

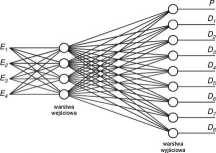
Rys.3.1. Struktura sieci diagnozującej.

Na wejścia sieci zostaną wprowadzone wartości czterech parametrów' z tabeli 4.1. Sieć posiadać będzie dziewięć wyjść: Dl + D8 i P. Wyjścia D1-HD8 będą wyprowadzać informację, czy wystąpił któryś z ośmiu defektów. Wyjście P zaś informację o poprawnej pracy alternatora. Wszystkie wyjścia będą zero-jedynkowe a funkcję aktywacji dla neuronów wybrano typu sigmoidalnego bipolarnego.

W końcowym rozdziale przedstawiono wyniki symulacji komputerowej opisanej wyżej sztucznej sieci neuronowej do diagnozowania alternatora na podstawie przedstawionych w tabeli 4.1 sygnałów uczących.

4. WYNIKI SYMULACJI KOMPUTEROWEJ

Próbki uczące i testowe są generowane losowo. Po pewnej obróbce przykłady tych ostatecznych zestawów próbek uczących przedstawiono w tabeli 4.1'.

Tabela 4.1.

Próbki uczące dla alternatora.

I.p	LI	L3	L2	L4	P	Dl	D2	D3	D4	D5	D6	D7	D8
1	1.342	1.342	0	0	1	0	0	0	0	0	0	0	0
2	1,320	1.320	0	0	1	0	0	0	0	0	0	0	0
3	1.276	1.276	0	0	1	0	0	0	0	0	0	0	0
4	1.286	1.286	0	0	1	0	0	0	0	0	0	0	0
5	1.320	1.320	0	0	1	0	0	0	0	0	0	0	0
6	1,274	1,274	0	0	1	0	0	0	0	0	0	0	0
7	1.345	1.345	0	0	1	0	0	0	0	0	0	0	0
8	1.278	1.278	0	0	1	0	0	0	0	0	0	0	0
50	1,301	1.354	1	0	0	0	0	0	0	0	1	0	0
51	1,291	1,317	1	0	0	0	0	0	0	0	1	0	0
52	1.196	1,322	1	0	0	0	0	0	0	0	1	0	0
53	1.280	1.348	1	0	0	0	0	0	0	0	1	0	0
54	1,256	1.321	1	0	0	0	0	0	0	0	1	0	0
55	1.213	1.363	1	0	0	0	0	0	0	0	1	0	0
56	1,262	1,337	1	0	0	0	0	0	0	0	1	0	0
57	1.326	1.180	0	1	0	0	0	0	0	0	0	1	0

Niektóre symulacje komputerowe przeprowadzili dyplomanci prof. A. Jastriebowa - A. Kaczmarek i B. Piwowar.

58	1.345	1.337	0	1	0	0	0	0	0	0	0	1	0
59	1.381	1.260	0	1	0	0	0	0	0	0	0	1	0
60	1,316	1,293	0	I	0	0	0	0	0	0	0	1	0
61	1,396	1.258	0	1	0	0	0	0	0	0	0	1	0
62	1.348	1.267	0	1	0	0	0	0	0	0	0	1	0
63	1,343	1.256	0	1	0	0	0	0	0	0	0	1	0
64	1.394	1.255	0	1	0	0	0	0	0	0	0	1	0
65	1,303	1.216	0	0	0	0	0	0	0	0	0	0	1
66	1.386	1.265	0	0	0	0	0	0	0	0	0	0	1
67	1,301	1.244	0	0	0	0	0	0	0	0	0	0	1
68	1.385	1.288	0	0	0	0	0	0	0	0	0	0	1
69	1,310	1,271	0	0	0	0	0	0	0	0	0	0	1
70	1.288	1,207	0	0	0	0	0	0	0	0	0	0	1
71	1.404	1.270	0	0	0	0	0	0	0	0	0	0	1
72	1,273	1.225	0	0	0	0	0	0	0	0	0	0	1
73	1,317	1.324	1	0	0	0	0	0	0	0	]	0	0
74	1.344	1.323	0	0	0	0	0	0	0	0	0	0	1
75	1,319	1.313	0	1	0	0	0	0	0	0	0	1	0
76	1,322	1.313	0	0	0	0	0	0	0	0	0	0	1

Stmktura sieci została wybrana dwuwarstwową (rys. 2.1, 5-11-4) z sigmoidalną bipolarną funkcją akty wacji neuronów. Dla uczenia stosowano pewną adaptacyjną wersję (ze stałym i zmiennym krokiem) algorytmu wstecznej propagacji (proces uczenia przy kładowo przedstawiono na tys. 4.1 i 4.2). a)    b)

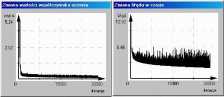
Rys. 4.1. a) i b) przedstawiają przebieg uczenia sieci algorytmem z krokiem dobieranym adaptacyjnie.

a)    b)

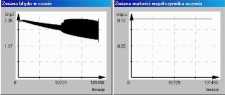
Rys. 4.2. a) i b) przedstawiają przebieg uczenia sieci algorytmem ze stałym krokiem.

Dla statystycznej analizy diagnozowania generowano po 100 próbek testowych, wyniki której przedstawiono na rys. 4.3 i 4.4.