79577725

* s.e wktor ^y.pr.^nu^w,8,td*^{łn CłMU Wekt}°' *»*>“*« ’ o‘^r«y^-

(1.4)

Stąd przyspieszenie ma wartość drugiej pochodnej skalarowe, drogi a(t> względem czasu    * ^łs'

a = f(t)    (i.₇₎

Na podstawie wzorów (1.4) i (1.6) należy stwierdzić, że wektory

prędkości i przyspieszenia są kolinearne z prosta U po której porusza się punkt.

tt ru.-hi* jednostajnym punktu droga » jest liniowa funkcja czasu óe

V ■ gy • const czyli do = udt

Po scalkowaniu powyższego równanU w przedziale odpowiadającym punktowi początkowemu 1 końcowemu, przy założeniu, że dla t_c = 0. e = a₀, otrzymamy

Ht • *ls) prosta równoległa do siecznej 1^*^. Odcinek OT mierzony w

"ka!i długości wyraża wartość prędkości średniej w jednostkach prędkości. Wartość prędkości chwilowej w punkcie K wyraża 8i« tsngcnsera kata $ nachylenia stycznej (2], Przy wyznaczaniu wartości przyspie-

»«en średniego i chwilowego na wykresie 9 * f(t) postępujemy analogie.nie jak pr.y znajdowaniu prędkości na wykresie t » f(t).

8

S As

t

v ;dt o

stad 8 ■ o₀ * ot

<!.•>

------ -v

W    jednootajnic «rlennyi* punktu prędkość jest liniowa funkcja

czasu

du

a * jy- • const czyli dti'» «dt

Całkując powyższe równanie w przedziale odpowiadającym punktem początkowemu i końcowemu otrzymamy

v    t

f dcJ ■ a S At V_Q    O

stad v = v₀ * at

Ponieważ prędkość jest równa

Przykład i, j. Dwa punkty poruszają sl» naprzeciw siebie wzdlui proetej ze zlał,ml prędkościami i»| i i>j. W jiewnej chwili punkty te zajmują położeni* 11 Im lej proste) I odległość miedzy nimi HH - f (rys. I.fzl. Pe przyjściu w punkcie * pwciąlku leru napisać równania ruchu dla kaidego punktu. OhlMayć czas Ig, po upływie którego punkty zk epotkają orzi znaletC drogi sj i *} przebycia punktów w lym ruska.

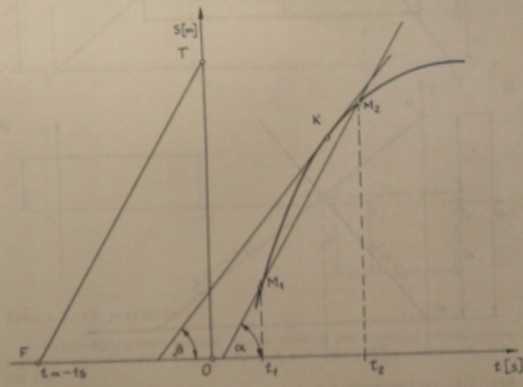
Nys. 1.1. WykreśIns przedstawienie ruchu |>unklu

♦ at

Całkując to^równanie w przedziale odpowiadającym punku- P~~«-kowemu i końcowemu, otrzymamy

/ de = no₀ * ^at)dt

*°    ° Iz

stąd s - *o ♦ •«* ⁺ l^at

(!.>•)

^D “ *0 •*    ⁺ j«**

W celu wykreślnego przedstawienia ruchu prostoliniowego przeanalizujmy wykres drogi s(t) pokazany na rys. 1.1. Wartość prędkości Średniej dla czasu At = tZ ~ *1 i^cs* ^ró»na tangensowi kąta pochylenia ziect

ncj przechodzącej przez punkty Afj i HW»rtoit tangensa kata i wyzna czarny z trójkąta 0S¥, gdzie odcinek FT otrzymano prowadzać z [>ur«:u

Równanie ruchu punktu M wynoel •i * *1*1

Równanie ruchu punktu I jest równe W chwili spotkania sis punktów z, s tj, stąd

*1*1- * * *l*K

Zatem czas **.po upływie którego punkty sl« spotkają, wynosi

4