22081

Zobaczmy jak będą wyglądały funkcje cena zbyt I producenta dla trzech różnych poziomów produkcji II producenta, gdy np. y₂ = 0; y₂ = 10; y₂ =20. Wtedy zgodnie z założeniem 4:

y₂=0=* p = -ay_i+b

y₂ = 10 => p = ~cy_l - 10a + b y₂ = 20 => p = -ay_{ - 20a + b

Wszystko to są proste o tym samym nachyleniu. Im większe y₂, tym prosta będzie leżała niżej. Prezentuje to rys. 1.

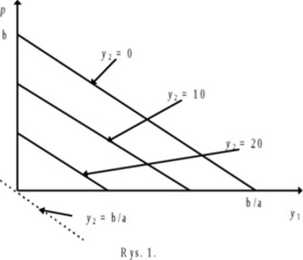
Łatwo można ustalić, że przez początek układu współrzędnych będzie przechodziła prosta o nachyleniu -a dla y₂ = b/a. To jest wielkość produkcji II producenta, przy której I producent nie ma już miejsca na danym rynku i nawet, gdyby obniżył cenę swojego produktu do 0, to i tak nic by nie sprzedał. Znając przebieg funkcji cena-zbyt możemy wykreślić przebieg przychodu krańcowego, który w tym przypadku będzie prostą wychodzącą z tego samego punktu przecięcia z osią ceny ale dwa razy bardziej stromą. Jeżeli dorysowalibyśmy dodatkowo przebieg funkcji kosztów krańcowych I producenta, to moglibyśmy stwierdzić, jaka jego wielkość produkcji zapewnia osiągnięcie mu maksymalnego zysku, gdy drugi producent będzie produkował określoną ilość dobra. W tym wypadku koszty krańcowe będą prostą, co widać we wzorze:

^K/=^H^o'^J)'^=2cy

Przedstawmy to na rys. 2.

dliy.= 20    dUy₂=0

dla 72=10

Rjs. 2.

Najpierw znajdujemy punkty przecięcia przychodu krańcowego i kosztów krańcowych. Realizują one nie tylko warunek konieczny na maksimum zysku ale również i warunek wystarczający, gdyż w każdym z nich nachylenie prostej K<’ jest większe od E'. W ten sposób znajdujemy wielkości