26065

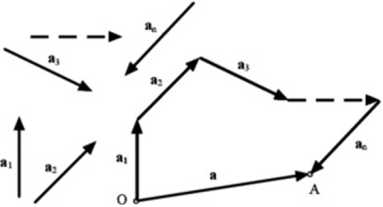
Rys. 2.7. Dodawanie n wektorów

Omówioną konstrukcję nazywamy wielobokiem wektorów. Jeżeli koniec ostatniego wektora pokrywa się z początkiem pierwszego, to suma wektorów jest równa zeru: a = 0. Mówimy wtedy, że wielobok jest zamknięty. W przeciwnym razie, tj. gdy a • 0, wielobok jest otwarty.

Czytelnikowi pozostawiamy wykazanie, że do dodawania wektorów stosuje się prawo pizemieiuiości:

a+ b = b+ a

oraz łączności

a+(b+c)= (a+ b) + c.

Aby analitycznie dodać n wektorów', musimy je wyrazić za pomocą współrzędnych z przyjętego układu współrzędnych:

^ak ^=ai«*^{+ a}kyJ⁺ (k = 1, 2,... n).

Po podstawieniu tego wzoru do równania (2.9) otizymamy:

n

k=l

n    n    n    n

= E(^ak«1+ a_ky J+ ^ k) I + J + ^k