30835

6. (tw. o działaniach arytmetycznych na granicach) Jeżeli lim a_n = a i lim b_n = b. to ciągi

n—oo    n— oo

(fln + b_n), (a„ - b_n), (a_nb_n),    b_n ^ 0 są zbieżne i

(a)    lim (a_n + b_n) = a + b

n—oo

(b)    lim («„ - b_n) = a -b

n—oo

(c)    lim (o„ • b„) = a • b

(d)    jeśli 6/0. to Hm ,(£)-£

Znane granice

1.    lim \/a = 1. dla o > 0;

n—oo

2.    lim tfu = 1;

n—oo

0    gdy    |a| < 1

3. lim o"

n—oo

1    gd y    « =    1

+oo    gdy    a >    1

nie istnieje gdy    a <    — 1

4.

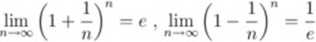
Oznaczenia

O = (a*o — S; #0 + S) - otoczenie punktu Xq € R o promieniu S

S = (aro — 6; aro) U (ar₀ ; ar₀ + 6) - sąsiedztwo punktu aro € R o promieniu 6 (aro — S; aro) - sąsiedztwo lewostronne punktu aro € R (ar₀; ar₀ + <$) sąsiedztwo prawostronne punktu ar₀ € R 6 - dowolnie mała liczba dodatnia.

Granica funkcji

Zał. Funkcja / jest określona w pewnym sąsiedztwie 5 = (aro — S; ar₀) U (ar₀; ar₀ + (5).

Def. Liczba g jest granicą funkcji / w punkcie ar₀ (ozn. lim /(ar) — g), jeśli spełniony jest jeden

x—io

z dwócli równoważnych warunków:

(1) Vc > 03tf > 0 [|x — ar₀| < 6 => |/(ar) — g\ < c) - def.Cauchy’go (2) V(ar_n) C S[(ar_n -► ar₀) => (f(x_n) — </)) - def.Heinego

Uwaga 1. Jeżeli istnieje ciąg (ar„) taki. że (ar_n —* a*o) A (f(x_n) —* gi) Agi ^ g. to Jim /(ar) ^ g.

Jeżeli istnieją dwa różne ciągi (ar’_n), (a*_n) takie, że

(ar'„ — ar₀) A {f(x_n) — g_x) i (ar^ — ar₀) A (f(x~_n) — &) oraz g_x f g₂,

2