5184
BAD_OPER02
Aby rozwiązać zadanie optymalizacyjne, należy narysować dowolną prostą o równaniu 400x, + 600x2 = C, gdzie C jest pewną stałą (wybieramy ją arbitralnie w ten sposób, żeby łatwo było narysować prostą np. weźmy tu C = 1200). Prosta 400x, + 600x2 =1200, czyli 2x,+3x2=6 wyznacza wszystkie punkty płaszczyzny, w których funkcja celu przyjmuje stałą wartość C. Prosta ta nazywa się warstwicą tzn. linią tych samych wartości funkcji celu. Jeżeli funkcja celu przyjmie inną wartość, to otrzymamy odpowiednią warstwicę przesuwając równolegle otrzymaną prostą.
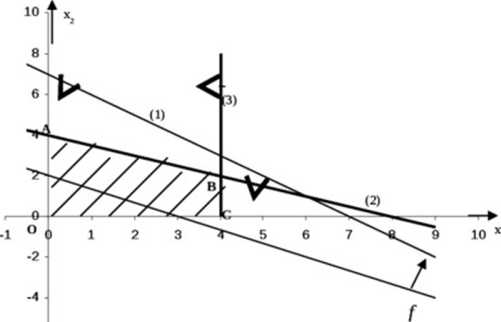
Rys.l. Rozwiązanie graficzne zadania 1
Ponieważ interesuje nas możliwie największa wartość funkcji celu, przesuńmy prostą równolegle w ten sposób, aby miała jeszcze punkty wspólne ze zbiorem rozwiązań dopuszczalnych. Otrzymujemy prostą mającą jeden punkt B=(4; 2), wspólny ze zbiorem dopuszczalnym. Prosta ma równanie 2x,+3x2=14, czyli 400x, + 600x 2 = 2800. W ten sposób znaleźliśmy rozwiązanie optymalne zadania x* =(4; 2) oraz maksymalną wartość funkcji celu fmn =2800.
Uwągą i
Kierunek, wzdłuż którego należy przesuwać równolegle prostą odpowiadającą funkcji celu, jest wyznaczony przez gradient . Dla funkcji liniowych gradient wyznacza się bardzo
łatwo. Jeżeli f(x,,x2)= c0 +c,x, +c
!X2» tO I j.
. Jest to wektor prostopadły do prostej
c0 +c,x, +c2x2 =0. Jeżeli interesuje nas minimalizacja funkcji celu na podanym zbiorze
2
Wyszukiwarka
Podobne podstrony:
DSC09121 Hiperbola o zadanych asymi I Rozwiązanie: I 4. Przez punkt K należy poprowadzić I dowolną p
DSC09121 Hiperbola o zadanych asymi I Rozwiązanie: I 4. Przez punkt K należy poprowadzić I dowolną p
egzaminD1 Dl 1 2 3 4 5 Suma Rozwiązanie zadania o numerze n należy napisać na n-tej stronie
Rozwiązanie a) = 2rr j = 2<t,j^—3a X 2a X-—-*■ Rozwiązywanie zadania zacząć należy od
Granica ciągu liczbowego Rozwiązanie: W zadaniu tym należy posłużyć się bardzo użyteczną techniką
Wojciech Grega, Metody Optymalizacji Rys. 1.5 Formułowanie i rozwiązywanie zadania optymalizacji Mod
Aby rozwiązać nierówność z niewiadomą x należy wyznaczyć zbiór tych wartości x, dla
DSC09092 Rozwiązanie: 2. Przez środek 5 okręgów jrt i należy poprowadzić dowolną prostą ę. Prze
DSC09117 Hiperbola o Udanych asymptoUch i danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowa
DSC09118 “danych asymptotachI danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowadzić do
DSC09092 Rozwiązanie: 2. Przez środek 5 okręgów jrt i należy poprowadzić dowolną prostą ę. Prze
DSC09117 Hiperbola o Udanych asymptoUch i danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowa
DSC09118 “danych asymptotachI danym punkcie Rozwiązanie: 1. Przez punkt A należy poprowadzić do
DSC09449 Prosta równoległa do płaszczyzny zadane) siadami Na płaszczyźnie a należy przyjąć dowolną p
S2-4 3 4 2 5 Rozwiązując zadanie techniką CORELAP należy znaleźć taką macierz permutacji:aby:
DSCN7085 (Kopiowanie) prawidłowo narysowanego wykresu ^)mówienie sposobu rozwiązywania zadania Narys
DSCN7102 (Kopiowanie) Biologia ^mówifliic sposobu rozwiązywania zadania Aby udzielić prawidłowej odp
DSCN7135 (Kopiowanie) Biologia £)mówicnie sposobu rozwiązywania zadania Aby wybrać odpowiednie argum
więcej podobnych podstron