083

Granica ciągu liczbowego

Rozwiązanie:

W zadaniu tym należy posłużyć się bardzo użyteczną techniką rozszerzania wyrażenia i wzorem skróconego mnożenia a² - b¹ = (a~ b) (a + b). Bierze się to stąd, że pojawia się tutaj nowy symbol nieoznaczony „co - ao”.

lim (ati + 10 - V/?) = „cc - oo” =

/f—>OC    V

^v    -jC

30

(\'/r + 10 - in) Nn + 10 + yn) (in + 10)- — (yn)²

= hm- ---= lim-.    -p— =

yn + 10 + yn    M-Mo in +10 + yn

= lim

10 -n

yn + 1 o -i- yn

■ = lim

10

yn- io + yń

zauważ, że korzystamy ze wzoru (a - b)(a + b) •■= + b¹

= 0

Zauważ, że mianownik ułamka    -p- jest coraz większy (bo n wzrasta

\n + 10 + V«

nieograniczenie), licznik się nie zmienia, zatem cały ułamek dąży do zera. Końcówkę zadania można rozwiązać jeszcze inaczej.

lim ,.... -    -- = lim

n-yrj \'/l + 10 + "Wl #-»»

I)

JO

r~

_\/7

yn + 1 o    yii

----1--—

V;?    in

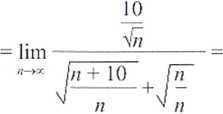
= lim

Odpowiedź

10

yń_

Hió    Z

+ — + yi n i

i

i

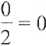
lim a = 0

n

n—yx.

ZADANIE 27__

Znajdź granicę a_r = V3n² + 10 - V3«² + 1

83