109782

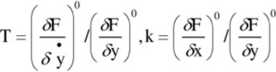
Opisany sposób linearyzacji odgrywa ważną rolę przy badaniu stabilności rozwiązań dla małych zmian parametrów wokół punktu równowagi (-* Lapunowa metody).

W analizie procesów periodycznych (drgań własnych) \stos. się linearyzację harmoniczną. W analizie procesów losowych stos. się linearyzację statystyczną.

schemat blokowy-

m rrf» Mtómj —J- zroąjeoy — kraik trat! jtt

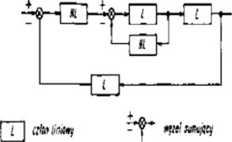
schemat układu z zaznaczeniem podziału na elementy i bloki funkcjonalne z uwzględnieniem ich właściwości dynamicznych przedstawiający oddziaływania między tymi elementami i blokami. Badając dynamikę procesów zachodzących w układach automatycznego sterowania abstrahuje się od zjawisk fizycznych stanowiących te procesy, interesujące są tylko ich modele matematyczne. S.b. składa się z członów stanowiących model matematyczny pewnych właściwości dynamicznych. Dlatego też dany układ automatycznego sterowania może być przedstawiony za pomocą różnych członów, a także jeden człon może odpowiadać procesom o różnym charakterze fizycznym. W każdym schemacie blokowym można wyróżnić cztery podstawowe elementy: człony liniowe lub nieliniowe o określonym

kierunku przepływu sygnału; człony porównujące (porównawcze) lub człony sumujące, w których następuje dodawanie lub odejmowanie sygnałów; węzły stanowiące punkty, w których następuje rozgałęzienie sygnału; linie skierowane przedstawiające kierunek przepływu sygnałów. Na rys. przedstawiono typowy schemat blokowy układu z zaznaczeniem tych elementów. S.b. można przekształcić do postaci najbardziej dogodnej z punktu widzenia prowadzonej analizy układu. Zasady przekształcania schematów blokowych noszą nazwę algebry schematów blokowych. S.b. spełniają bardzo ważną rolę w analizie układów automatycznego sterowania.

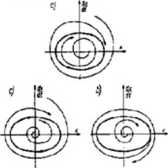
Cykl graniczny — zamknięta trajektoria fazowa obejmująca położenie równowagi. Krzywej tego typu odpowiadają ustalone drgania okresowe układu