116461

Kategorie modeli matematycznych

•    deterministyczne i stochastyczne,

•    statyczne i dynamiczne,

•    ciągłe i dyskretne,

•    kwantowe i skończone,

•    stacjonarne i niestacjonarne,

•    liniowe i nieliniowe.

Model deterministyczny - dla każdej jednej wielkości wejściowej istnieje jedna wielkość wyjściowa (zależności pomiędzy zmiennymi modelu są ściśle określone).

Model stochastyczny - dla każdej jednej wielkości wejściowej istnieje wiele wielkości wyjściowych (zależności między zmiennymi modelu są opisane przez rozkłady prawdopodobieństwa) - np. czy wzrost dziecka zależy od wieku

Model dynamiczny - wyjście zależy od wejścia w całym nieskończonym poprzedzającym przedziale czasowym V (u, t) = y (u(x): -<*> < t £ t}

Model statyczny - zakłada rozpatrywanie układu w stanie ustalonym (pomija stan wcześniejszy) - określone są tylko zależności funkcyjne między wejściem a wyjściem

•o»
«*•
	. f *
	*	•' i

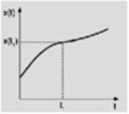
Model ciągły - wartości zmiennych modelu są określone w każdej chwili czasu. Czas zmienia się w sposób ciągły, więc zbiór wszystkich wartości zmiennych czasu jest niepoliczalny. Model ten zapisujemy za pomocą równań różniczkowych zwyczajnych lub cząstkowych

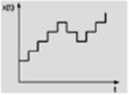
Model dyskretny - wartości zmiennych modelu są określone w dyskretnych chwilach czasu. Model taki opisujemy za pomocą równań różnicowych.

Model kwantowy - zmienne modelu przyjmują tyłko określone wartości

Model skończony - zmienne przyjmują tyłko skończoną liczbę wartości

Model stacjonarny - model, którego parametry nie zmieniają się w czasie.

Model niestacjonarny - parametry modelu zmieniają się w czasie.

Model nieliniowy - opisany nieliniowymi równaniami (różniczkowymi/różnicowymi) Model liniowy - opisany liniowymi równaniami (uproszczenia nieliniowych)