123598

(8.4)

_k ( _±±£, ^

^r J

Jeżeli wartości k i (5 dobraliśmy tak, aby

kp> 1    (8.5)

to jak wynika ze wzoru (8.4), sygnał y(t)narastałby do nieskończoności, gdyby wzmocnienie wzmacniacza k w całym zakresie pracy układu było stałe.

Praktycznie biorąc charakterystyka wzmacniacza jest zawsze ograniczona nasyceniem. Dlatego wzmocnienie k ze wzrostem sygnałów maleje i narastanie skończy się dla takiej wartości -*i„. dla której k =1/ fi. Ilustruje to rysunek 8.5. Jeżeli został wzbudzony, tzn. jego stan określony jest przez punkt A, to dla przejścia od wartości y =y_n ponownie do wartości y=0 należy do węzła sumacyjnego doprowadzić sygnał ujemny o wartości bezwzględnej większej od *i„. Wynika stąd przebieg statycznej cliarakterystyki układu pokazany na rys. 8.6. Jest to charakterystyka przekaźnika dwupołożeniowego za strefą niejednoznaczności *m. O wartości strefy niejednoznaczności decyduje wartość funkcji przejścia fi zastosowanego sprzężenia zwrotnego.

Przesunięcie charakteiystyki (rys.8.6) wzdłuż osi x można uzyskać, wprowadzając do węzła sumacyjnego sygnał pokazujący ■*„. Charakterystyka statyczna układu ma wówczas kształt pokazany na rys. 8.7.

Dla uzyskania przekaźnika trójpołożeniowego należy zestawić dwa układy omawiane poprzednio w sposób pokazany na rys.8.8.

Jako przykład praktycznego wykorzystania przekaźnika bezstykowego pokazany jest na iys. 8.9 schemat bezstykowego przekaźnika magnetycznego. Do jego konstrukcji wykorzystano dwa wzmacniacze magnetyczne o układzie szeregowym, w których dla uzyskania działania przekaźnikowego zastosowano dodatnie sprzężenie zwrotne prądowe.

8.2. Funkcja opisująca przekaźniki trój położeniom e.

Przekaźnik trójpołożeniowy jest jak wynika z bezpośrednio z jego charakteiystyki, elementem nieliniowym. Dla zanalizowania pracy układu automatyki, w którym przekaźnik zostanie zastosowany, trzeba będzie więc korzystać z którejś z metod analizy układów nieliniowych, np. metody pierwszej harmonicznej lub metody płaszczyzny fazowej. Stosując metodę pierwszej harmonicznej należy znać tak zwaną funkcję opisującą dany element nieliniowy, określona wzorem (7.14). Obliczymy tę funkcję dla przekaźnika trójpołożeniowego bez strefy niejednoznaczności, tylko ze strefą nieczułości a. Charakterystyka statyczna takiego przekaźnika przedstawiona jest na rys. 8.10.

Aby obliczyć funkcję opisującą ten przekaźnik, rozpatrzymy przebieg sygnału wyjściowego y, wywołany wprowadzeniem na wejście sygnału sinusoidalnego x = A sin ca. Przebieg ten jest pokazany na rysunku 8.11. Ponieważ przyjęliśmy jednoznaczną charakterystykę przekaźnika, więc na podstawie wzoru (7.16) jest C₂ = 0. Dla obliczenia funkcji opisującej należy znaleźć tylko współczynnik C, według wzoru (7.15):

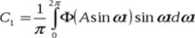
Na podstawie rysunku 8.11 jest: