89521 s32 33

32

8. Wyznaczyć wartości parametru b tak, aby funkcja

/(*) =

sin2x dla x < 0, bx dla x > 0

była wszędzie różniczko walna.

Pozostaje zbadać różniczkowalność funkcji / jedynie w punkcie x₀ pozostałych punktach x e 1R\ {0} jest ona funkcją różniczkowalną.

= 0, gdyż w Mamy więc

/'(0-) = lim    = lim

Aj*—0~    Ax    Aj:—0~

= Um    = 2,

Aj:—0“ 2Ax

sin2Ax

Ax

i

/’<0+) = lim ^/(Ał|' -^/(0) = lim p

Aj:—0+    Ax    Aj* —0+ Ax

Stąd wynika, że /'(O) istnieje jedynie wtedy, gdy b — 2. Odp. Dla b — 2, funkcja. / jest wszędzie różniczkowalna.

- b

9. Zbadać różniczkowalność funkcji y(x) — 2x -f \x — 1|

w punkcie xq = 1.

Korzystając z definicji wartości bezwzględnej

x

ii

x — 1    dla x > 1,

— (x — 1) dla a: < 1,

marny

V =

2x + x — 1 dla a; > 1, 2x — (x — 1) dla x < 1,

a więc

V =

3.x — 1 dla x > 1, x 4- 1 dla x < 1.

Obliczmy pochodne jednostronne funkcji y w punkcie x₀ — 1. Zgodnie z defini cją, mamy

,,, _N    j/(l + Aa;) - j/(l)    1 + Ax + 1 - 2    ,

7/(1-) = lim -r- s lun --- = 1,

Aj:—0“    Ax    A J—0    Ax

lim

Ar —^0+

2/(1 + Ai) - y(l)

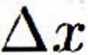
3(1 + Az) - 1 - 2 Ax

Stąd y'( 1—) ^ y'( 1+), a więc funkcja y nie jest różniczkowalna w punkcie xq = 1.

10. Napisać równania stycznych i normalnych do krzywej y — 6x — x² w punktach jej przecięcia się z osią Ox.

Równania stycznej i normalnej do krzywej y = f(x) w punkcie Po(xq, /(to)) są odpowiednio postaci:

y-.f(x₀) = f'(x₀)(x - x₀) równanie stycznej,

IJ — f(xo) — “ttt—— To) równanie normalnej,

f'\^x o)

gdy /'(.to) 7^ 0. Funkcja y przecina oś Ot w punktach Pi (0,0), P2(6,0). Oczywiście, y'(x) — 6 — 2t, a więc y'(0) = 6, oraz y'{6) = —6. Stąd mamy dwa równania stycznych:

y — 6t oraz y — —6x -f 36.

Podobnie otrzymujemy równania normalnych:

1 1 ,

7/ — —x oraz y — —x — 1 ^J 6 6

11. Na paraboli y = x² -f 3, znaleźć punkty w których styczna jest równoległa do (a) osi Ot, (b) prostej y = 4t + 10.

Ponieważ, y^r = 2x, więc m = 2xq jest współczynnikiem kierunkowym stycznej do paraboli y — x² + 3 w punkcie to leżącym na tej paraboli.

(a)    ;// — 0 jest równaniem osi Ot, a więc 2t₀ = 0, czyli tq — 0. Podstawiając To = 0 do równania paraboli, mamy y₀ = 3, a więc P(0,3) jest szukanym punktem.

(b)    Ponieważ proste równoległe mają równe współczynniki kierunkowe, więc 2t₀ = 4, a stąd t*o — 2. Teraz P(2, 7) jest szukanym punktem.