49427

w Cu

Wyobraźmy sobie fikcyjny sześcian o długości hoku a (przedstawiony iw rysunku linią przerywaną). Pięty AB i UC mają kierunek poziomy. Kręt AH jest zamocowany w punkcie A a pręt BO w punkcie O. Kret BI) ma kierunek pionowy i jest zamocowany w punkcie D. Wszystkie trzy pręty są. połączone przegubem B. Przegub B obciąża siła P, która ma kierunek odcinka BE. Należy obliczyć siły w prętach AB, BC i BD.

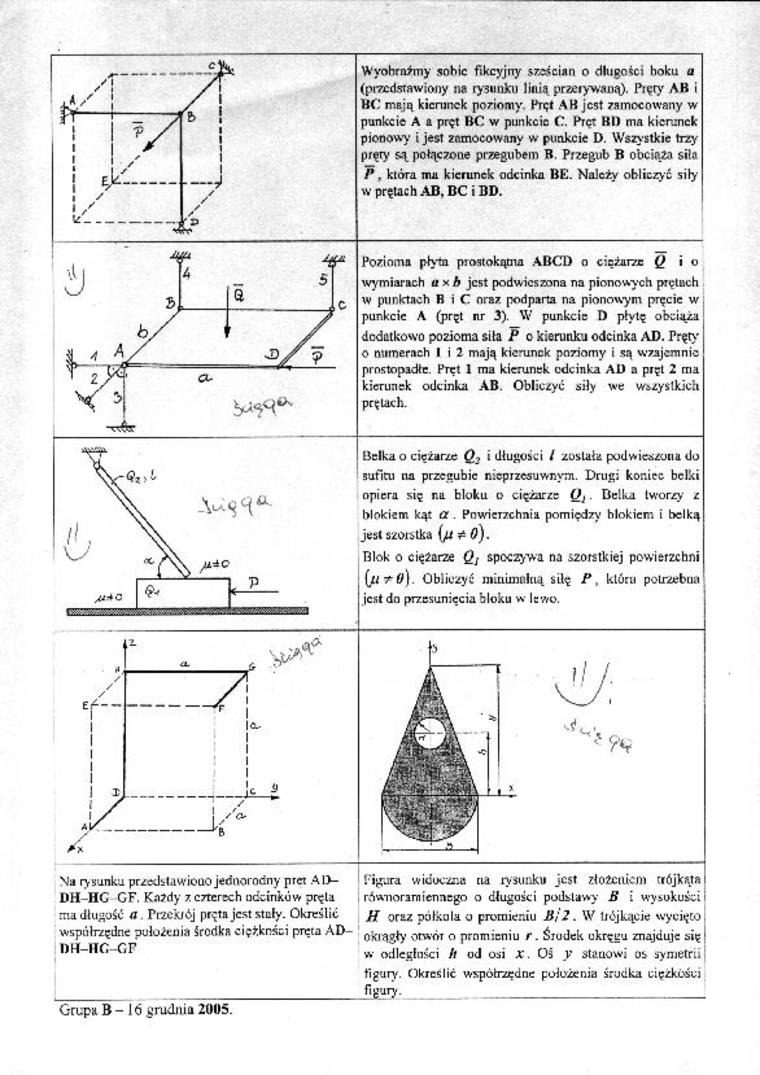
Kozinma płyta piostokąma ABOD o ciężarze Q i o wymiarach ux b jest podwieszona na pionowych pietach w punktach B i C. oraz podparta na pionowym pręcie w punkcie A (pręt nr 3). W punkcie D płytę obciąża

dodatkowo pozioma siła P o kierunku odcinka AD. Pręty O numerach I i 2 mają kierunek poziomy i są wzajemnie prostopadłe. Kręt 1 ma kierunek edeinka AD a pręt 2 ma kierunek odcinka AB. Obliczyć siły we wszystkich prętach.

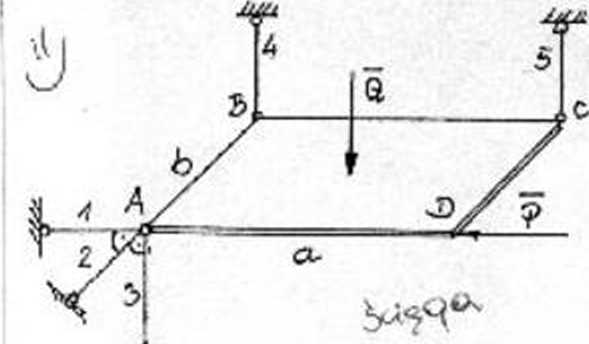
Belka o ciężarze Q₂ i długości / została podwieszona do sufitu tui przegubie nteprzesuwnym. Drugi kor.iec belki opiera się na bloku o ciężarze Qj. Belka tworzy z blokiem kąt a . KnwieTzchnia pomiędzy blokiem i belką jest szotslka (p * 0).

Blok o ciężarze Q_s spoczywa na szorstkiej powierzchni [ll t 01. Obliczyć iiiiuimnluą silę P, któru polrzebua jest dn przesunięcia bloku w lewo.

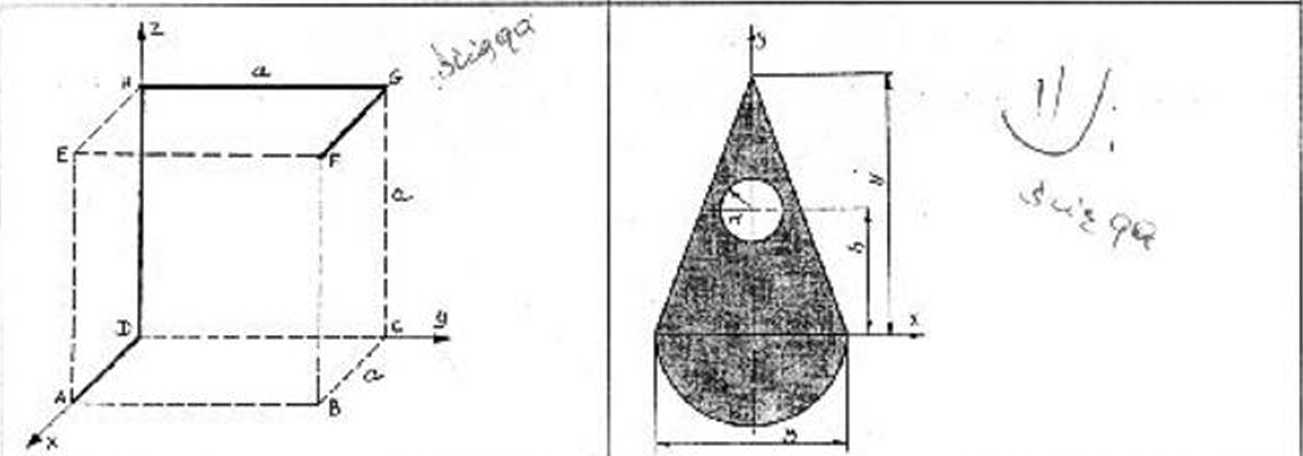
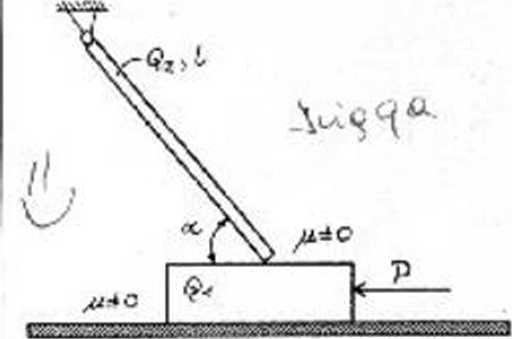
Na rysunku przedstawiono jednorodny pret Al)-    Figura widoczna na rysunku jest złożeniem Trójkąta

DH-HG GF. Każdy z czterech ućeinkuw pręta    równoramiennego o długości podstawy B i wysukuścii

ma długość a Przckfój pręta jest stuły. Określić    }f oraz półkula o promieniu Bi 2. W trójkącie wycięto,

współrzędne pułożtruia środka ciężkości pręta AD- Ciągły otwór o promieniu r. Śiudek ukręou znajduje się¹ IW-IIC-GP    _w ocllcgliiści h od osi x. Oś V stauowi os symetr:.

figury. Określić współrzędne położenia śrudka ciężkości figury. ___

Grupa B - 16 grudnia 2005.