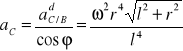Kolokwium wykładowe z kinamatyki
1. Obliczyć wartość iloczynu skalarnego ![]()
wektorów o składowych ![]()
i ![]()
.
Odp.: ![]()
.
2. Obliczyć wartość iloczynu wektorowego ![]()
wektorów o składowych ![]()
i ![]()
.
Odp.: 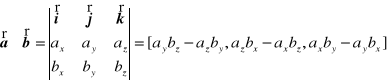
.
3. Obliczyć wartość iloczynu mieszanego ![]()
wektorów o składowych ![]()
, ![]()
i ![]()
.
Odp.:
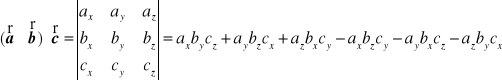
.
4. Uprościć wyrażenie: ![]()
.
Odp.: Na podstawie tożsamości ![]()
wnioskujemy ![]()
.
5. Uprościć wyrażenie: ![]()
.
Odp.: ![]()
. Na podstawie antyprzemienności iloczynu mieszanego wnioskujemy, że ![]()
. Stąd wynika ![]()
.
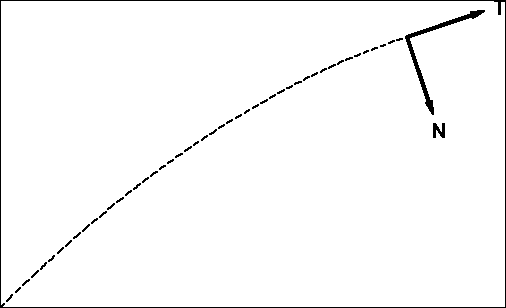
6. Sformułuj i objaśnij twierdzenie o rozkładzie przyspieszenia punktu na przyśpieszenie normalne i styczne.
Odp.: ![]()
gdzie ![]()
jest przyspieszeniem stycznym, ![]()
jest przyśpieszeniem normalnym, ![]()
jest jednostkowym wektorem stycznym, ![]()
jest krzywizną toru, ![]()
jest promieniem krzywizny toru, ![]()
jest jednostkowym wektorem normalnym.
7. Dane są równania płaskiego ruchu punktu materialnego: ![]()
gdzie ![]()
i ![]()
są stałymi. Wyznaczyć przyspieszenie normalne i styczne w chwili ![]()
.
Odp.: 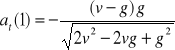
, 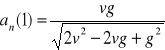
.
Obliczenia: Na podstawie twierdzenia o rozkładzie przyspieszenia punktu na przyśpieszenie normalne i styczne obliczmy:
a). Wektor prędkości punktu ![]()
.
b). Długość wektora prędkości ![]()
.
c). Jednostkowy wektor styczny 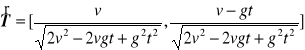
.
d). Jednostkowy wektor normalny 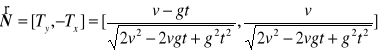
, bo w ruchu płaskim wystarczy obrócić ![]()
o -90o aby otrzymać ![]()
.
e). Wektor przyśpieszenia ![]()
.
f). Przyspieszenie styczne 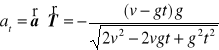
.
g). Przyspieszenie normalne 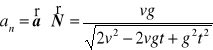
.
h). Wartości chwilowe przyspieszenia stycznego i normalnego:
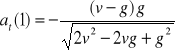
, 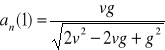
.
8. Sformułuj i objaśnij twierdzenie o prędkościach i przyśpieszeniach punktów bryły w ruchu kulistym.
Odp.: W ruchu kulistym prędkość i przyśpieszenie punktu bryły o położeniu ![]()
względem środka ruchu wynoszą odpowiednio
![]()
, ![]()
gdzie ![]()
jest wektorem prędkości kątowej bryły, a ![]()
jest wektorem przyśpieszenia kątowego bryły?
9. Wiadomo, że bryła porusza się ruchem obrotowym ze stałą prędkością kątową ![]()
. Obliczyć składowe wektorów prędkości i przyśpieszenia punktu bryły o współrzędnych ![]()
względem układu współrzędnych z zerem na osi obrotu.
Odp.: ![]()
, ![]()
.
Z twierdzenia o prędkościach punktów bryły w ruchu kulistym wynika, że prędkość rozpatrywanego punktu wynosi
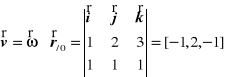
Z twierdzenia o przyśpieszeniach punktów bryły w ruchu kulistym wynika, że przyśpieszenie rozpatrywanego punktu wynosi
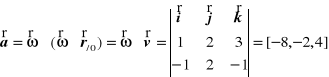
bo ![]()
.
10. Wiadomo, że bryła porusza się ruchem kulistym, a punkty A i B mają współrzędne odpowiednio [1,0,0] i [0,1,0] względem układu współrzędnych z zerem w środku ruchu kulistego. Wiadomo również, że składowe prędkości punktów A i B wynoszą odpowiednio [0,3,-2] i [-3,0,1] w tym samym układzie współrzędnych. Wyznaczyć składowe wektora prędkości kątowej bryły.
Odp.: ![]()
.
Obliczenia: Z twierdzenia o prędkościach punktów bryły w ruchu kulistym zastosowanego dla punktów A i B wynika
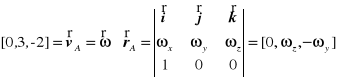
,
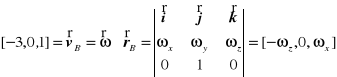
.
Stąd wnioskujemy, że ![]()
, ![]()
, ![]()
jest rozwiązaniem otrzymanego układu równań.
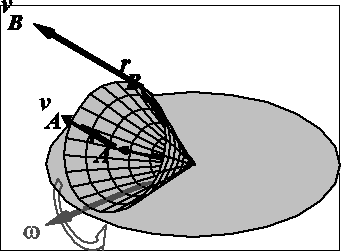
11. Stożek prawidłowy o wysokości h i rozwartości 2 toczy się bez poślizgu po poziomej płaszczyźnie. Wiadomo, że wartość bezwzględna wektora prędkości kątowej stożka jest stała i wynosi ![]()
. Oblicz wartość bezwzględną prędkości środka podstawy stożka / najwyższego punktu podstawy stożka.
Odp.: ![]()
/![]()
.
Obliczenia: Z warunków zadania wynika, że stożek porusza się ruchem kulistym wokół swego wierzchołka a linia kontaktu stożka z płaszczyzną jest osią chwilowego obrotu stożka. Zatem prędkość punktu A obliczmy ze wzoru
Zatem wartość bezwzględna prędkości punktu A wynosi
Dla punktu B jest podobnie
|
|
12. Stożek prawidłowy o wysokości h i rozwartości 2 toczy się bez poślizgu po poziomej płaszczyźnie. Wiadomo, że wartość bezwzględna wektora prędkości kątowej stożka jest stała i wynosi ![]()
. Oblicz wartość przyśpieszenia środka podstawy stożka.
Odp.: ![]()
.
Obliczenia: Z warunków zadania wynika, że stożek porusza się ruchem kulistym wokół swego wierzchołka a linia kontaktu stożka z płaszczyzną jest osią chwilowego obrotu stożka. Zatem prędkość środka podstawy obliczmy ze wzoru ![]()
, gdzie ![]()
jest wektorem położenia środka podstawy względem wierzchołka. jej wartość bezwzględna wynosi ![]()
i jest stała. Zatem przyśpieszenie styczne środka podstawy jest równe zeru.
Środek podstawy porusza się po okręgu o promieniu ![]()
. Zatem jego przyśpieszenie normalne wynosi ![]()
.
13. Stożek prawidłowy o wysokości h i rozwartości 2 toczy się bez poślizgu po poziomej płaszczyźnie. Wiadomo, że wartość bezwzględna wektora prędkości kątowej stożka jest stała i wynosi ![]()
. Znajdź wektor przyśpieszenia kątowego stożka.
Odp.: ![]()
. A JEDNAK NIE ZERO.
Obliczenia: Z warunków zadania wynika, że stożek porusza się ruchem kulistym wokół swego wierzchoła a linia kontaktu z płaszczyzną jest osią centralną chwilowego obrotu stożka. Z kinematyki ruchu kulistego wynika, że środek podstawy stożka A ma prędkość ![]()
, oraz ![]()
. Z drugiej strony środek postawy porusza się po okręgu ze stałą kątową prędkością (precesji) ![]()
. Stąd wynika ![]()
, ![]()
oraz ![]()
. Z taką samą prędkością kątową porusza się koniec wektora ![]()
. Zatem traktując wektor ![]()
jako wektor położenia swego końca mamy ![]()
oraz ![]()
.
14. Sformułuj i objaśnij twierdzenie o prędkościach i przyśpieszeniach punktów bryły.
Odp.: Prędkość i przyśpieszenie punktu bryły o położeniu ![]()
względem innego punktu A bryły wynoszą odpowiednio
![]()
, ![]()
gdzie ![]()
jest wektorem prędkości kątowej bryły, a ![]()
jest wektorem przyśpieszenia kątowego bryły.
15. Wiadomo, że punkty A, B i C o współrzędnych [0,0,0], [1,0,0] i [0,1,0] mają prędkości o składowych odpowiednio [1,1,2], [1,3,1] i [-1,1,3] w tym samym układzie współrzędnych. Wyznaczyć składowe wektora prędkości kątowej bryły.
Odp.: ![]()
.
Obliczenia: Korzystamy ze wzorów ![]()
i ![]()
otrzymując następujący układ równań ![]()
=0, ![]()
=0.
16. Koło o promieniu R toczy się ruchem płaskim po płaszczyźnie bez poślizgu. Wiadomo, że prędkość środka koła ![]()
jest stała. Wyznaczyć przyspieszenie punktu odległego o r od środka koła w swym najwyższym/najniższym/dowolnym położeniu.
Odp.: ![]()
.
Obliczenia.
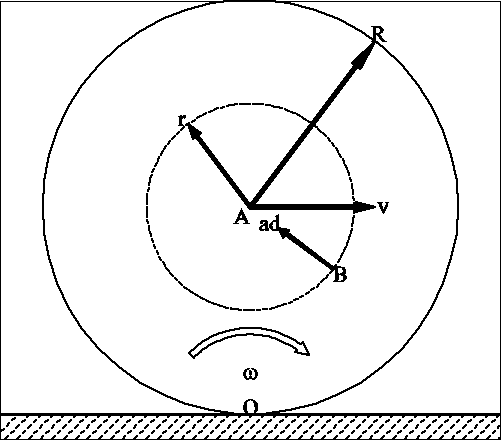
Z twierdzenia o prędkościach punktów bryły ![]()
, bo ![]()
.
Zatem prędkość kątowa koła wynosi ![]()
. Zatem przyśpieszenie kątowe koła wynosi ![]()
.
Z twierdzenia o przyśpieszeniach punktów bryły ![]()
. Ale przyśpieszenie środka koła wynosi ![]()
. Przyśpieszenie obrotowe również znika ![]()
. Pozostaje jedynie przyśpieszenie dośrodkowe ![]()
.
Uwaga! Jak to zwykle bywa w niniejszym zadaniu przyśpieszenie środka chwilowego obrotu jest niezeroweeeeeeeeeeeeeeeee i wynosi ![]()
.
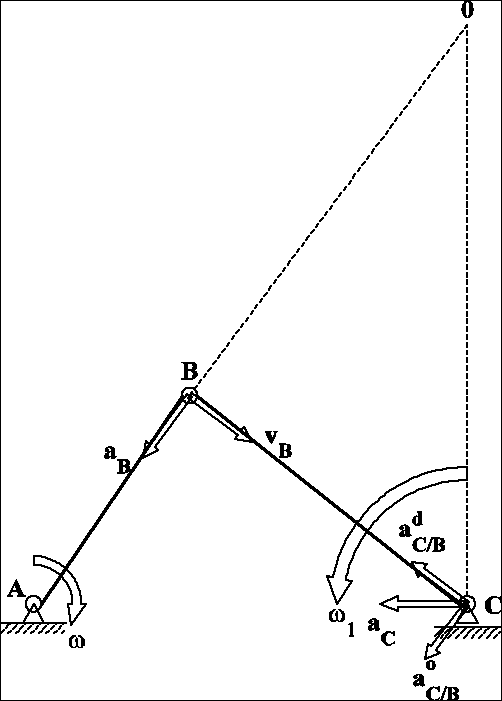
17. Korba o długości r układu korbowego obraca się ze stałą prędkością kątową . Obliczyć wartości przyśpieszeń końca korbowodu w jednym z jego skrajnych położeń. Założyć, że długość korbowodu l>r.
Odp.: ![]()
.
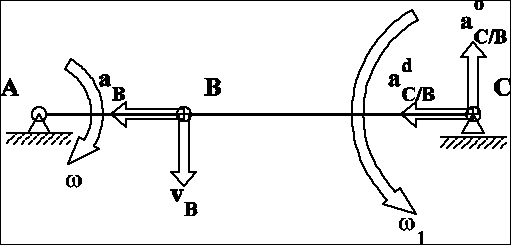
Obliczenia: Z ruchu obrotowego korby wynika ![]()
i ![]()
. Z więzów korbowodu wynika, że C jest środkiem chwilowego obrotu korbowodu. Ze wzoru ![]()
wynika zatem prędkość obrotowa ![]()
korby oraz przyśpieszenie ![]()
dośrodkowe punktu C względem B. Wobec wzoru ![]()
oraz więzów wynika , że przyśpieszenie obrotowe punktu C względem A ![]()
. Zatem ![]()
oraz ![]()
.
18. Korba o długości r układu korbowego obraca się ze stałą prędkością kątową . Obliczyć wartości przyśpieszeń końca korbowodu w położeniu, w którym korba jest prostopadła do korbowodu. Założyć, że długość korbowodu l>r.
Odp.:
Obliczenia: Z ruchu obrotowego korby wynika
|
|
19. Sformułuj i objaśnij twierdzenie o prędkościach w ruchu złożonym punktu.
Odp.: Jeżeli równania ruchu punktu materialnego przedstawić w postaci
![]()
gdzie ![]()
są współrzędnymi rozpatrywanego punktu względem zaczepionego w punkcie ![]()
ruchomego układu współrzednych o wersorach ![]()
to prędkość bezwzględna punktu wynosi ![]()
gdzie
![]()
jest prędkością względną, a
![]()
jest prędkością unoszenia, natomiast ![]()
jest wektorem prędkości kątowej ruchomego układu współrzędnych.
20. Sformułuj i objaśnij twierdzenie o przyśpieszeniach w ruchu złożonym punktu.
Odp.: Jeżeli równania ruchu punktu materialnego przedstawić w postaci
![]()
gdzie ![]()
są współrzędnymi rozpatrywanego punktu względem zaczepionego w punkcie ![]()
ruchomego układu współrzednych o wersorach ![]()
to przyspieszenie bezwzględne punktu wynosi ![]()
gdzie
![]()
jest przyśpieszeniem względnym,
![]()
jest przyśpieszeniem unoszenia, a
![]()
jest przyspieszeniem Coriolisa natomiast ![]()
i ![]()
są wektorami prędkości i przyspieszenia kątowego ruchomego układu współrzędnych.
Wyszukiwarka
Podobne podstrony:
Kinematyka, Imię i nazwisko:
Imię i nazwisko
fizyka dynamika - pr klasowa, Imię i nazwisko:
okulistyka wejsciowki gielda, Test+z+anatomii+grupa++++++październikowa, Imię nazwisko…&helli
Sprawozdanie 11, Imię i nazwisko
III Klasa, 4.IIIB.Grupa B(PP), Grupa B Imię i nazwisko ucznia
test-pokarmowy-1, IMIĘ I NAZWISKO:
test, Imię i nazwisko
testy, MobCom 2006 F, Imię i nazwisko
Ćw nr 45, 45, Imie Nazwisko
testy, MobCom 2006 D, Imię i nazwisko
7 Chromatografia jonowymienna, 7. chromatografia jonowzmienna, Imię i nazwisko
kartkowka 4, obwód prostokąta i kwadratu, Imię i Nazwisko:
fizyka-energia, Imię i nazwisko:
Wersja B Nerwy i zmysły 2010 Imię i Nazwisko, Spradziany
GPw UE Zestaw pytan 2011 Heffner, Imię i Nazwisko:
S2, 1.Grupa A, Grupa A Imię i nazwisko ucznia
Zadania dr Marty Kuc, spr4, Imię i nazwisko: ………………&hellip
więcej podobnych podstron