Metoda węgierska.

Rozwiązanie zagadnienia przydziału.

1. Wstęp

Załóżmy, że istnieje n różnych czynności, które mogą zostać wykonane przez n mechanizmów. Każdy mechanizm może wykonać tylko jedną czynność z różnym skutkiem. Należy przydzielić czynności do mechanizmów w taki sposób, aby wynik był optymalny.

Np.

Kierownik ma za zadanie rozdzielić n czynności A₁, A₂,..., A_n pomiędzy n pracowników P₁, P₂,..., P_n. Każdy pracownik wykonuje daną czynność z odpowiednim do swoich kwalifikacji efektem. Założono, że wiersze odpowiadają pracownikom, kolumny czynnościom, natomiast wartości macierzy odpowiadają zyskom, jakie może wypracować każdy pracownik wykonując odpowiednie czynności. Założenia możliwości przydziału zapisano w macierzy C.

Np. pracownik trzeci wykonuje czynność pierwszą z efektem 5, czynność drugą z efektem 4, itd...

Obowiązkiem kierownika jest taki przydział czynności, aby sumaryczny wynik pracy był maksymalny. Należy, więc z każdego wiersza i każdej kolumny wybrać dokładnie po jednym elemencie tak, aby ich suma był największa.

Gdyby macierz C była zbudowana tak, że maksymalne elementy jej wierszy znajdowałyby się w różnych kolumnach, rozwiązanie problemu byłoby proste. Na ogół jednak, kilka maksymalnych elementów różnych wierszy znajduje się w jednej i tej samej kolumnie lub odwrotnie. Wówczas rozwiązanie problemu nie jest oczywiste szczególnie, gdy wymiar problemu jest duży.

Metoda węgierska polega na wykonaniu kroku przygotowawczego oraz skończonej ilości iteracji. Każda iteracja przybliża o jeden element rozwiązanie optymalne. Rozwiązanie problemu maksymalizacji i minimalizacji różni się jedynie krokiem przygotowawczym. Dalsze obliczenia są identyczne.

Przyjęto, że elementy są niezależne, jeżeli w jednym wierszu i jednej kolumnie znajduje się tylko jeden element z danego zbioru. Zagadnienie przydziału polega na wyborze n elementów niezależnych z macierzy opisującej problem, których suma jest optymalna (minimalna lub maksymalna w zależności od problemu). Rozmieszczenie elementów niezależnych wskazuje na rozwiązanie optymalne.

Wyjaśnienie metody węgierskiej zrealizowane zostanie w oparciu o w/w przykład.

2. Rozwiązanie problemu

2.1 Krok przygotowawczy

2.1.1 Maksymalizacja

• Określa się maksimum elementów z każdej kolumny:

• Przekształca się macierz C do równoważnej macierzy C'=[c'_ij] gdzie
  

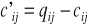
• Określa się minimum elementów z każdego wiersza:

• Przekształca się macierz C' do równoważnej macierzy C⁰=[c⁰_ij] gdzie
  

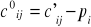
• Otrzymano w ten sposób w każdym wierszu i w każdej kolumnie przynajmniej jedno zero. Oznacza się gwiazdką dowolne zero w pierwszej kolumnie (0^*). Następnie przegląda się drugą kolumnę i jeżeli znajduje się w niej zero należące do wiersza, w którym brak jest 0^*, to oznacza się to zero (0^*). Analogicznie przegląda się pozostałe kolumny macierzy C⁰. Wyznaczono w ten sposób zera niezależne. Ważnym jest przyjęcie kierunku analizy macierzy i konsekwentne jej stosowanie aż do uzyskania rozwiązania.

2.1.2 Minimalizacja

• Określa się minimum elementów z każdej kolumny:

• Przekształca się macierz C do równoważnej macierzy C'=[c'_ij] gdzie
  

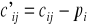
• Określa się minimum elementów z każdego wiersza:

• Przekształca się macierz C' do równoważnej macierzy C⁰=[c⁰_ij] gdzie
  

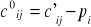
• Otrzymano w ten sposób w każdym wierszu i w każdej kolumnie przynajmniej jedno zero. Oznacza się gwiazdką dowolne zero w pierwszej kolumnie (0^*). Następnie przegląda się drugą kolumnę i jeżeli znajduje się w niej zero należące do wiersza, w którym brak jest 0^*, to oznacza się to zero (0^*). Analogicznie przegląda się pozostałe kolumny macierzy C⁰. Wyznaczono w ten sposób zera niezależne. Ważnym jest przyjęcie kierunku analizy macierzy i konsekwentne jej stosowanie aż do uzyskania rozwiązania.

2.2 Iteracja

Założono, że została wykonana k-ta iteracja w wyniku, której określona jest równoważna macierzy C⁰ macierz C^k=[c^k_ij], c^k_ij>= 0.

Należy sprawdzić, czy macierz C^k zawiera n zer niezależnych. Jeżeli tak, to otrzymano rozwiązanie optymalne (optymalny wybór określony jest pozycjami zer niezależnych (0^*)). W przeciwnym przypadku przeprowadza się k+1 iterację.

Wszystkie kolumny macierzy C^k zawierające 0^* wyróżnia się znakiem + (wyróżnienie kolumny lub wiersza znakiem + oznacza wyróżnienie wszystkich elementów tej kolumny lub wiersza).

Krok 1

Przyjęto, że analiza macierzy odbywać się będzie kolumnami od lewej strony. Można przyjąć inaczej, ale konsekwentnie do uzyskania rozwiązania optymalnego.

Jeżeli w pierwszej (od lewej strony) kolumnie nie wyróżnionej (+) znajduje się zero, to wydziela się je znakiem 0' (jeżeli nie ma takiego zera, to analizuje się kolejno następne elementy tej kolumny oraz kolumny następne).

Jeżeli wiersz zawierający wyróżnione 0' nie zawiera 0^*, to należy przejść do kroku 2. Jeżeli natomiast zawiera 0^*, to należy wyróżnić wiersz (+), a skasować wydzielenie kolumny, w której znajduje się 0^* leżące w analizowanym wierszu.

W taki sposób należy wyróżnić wszystkie, możliwe ze względu na założone kryteria 0.

Po wydzieleniu wszystkich 0, należy przejść do kroku 3.

Krok 2

Określenie łańcucha zer.

Zaczynając od ostatnio wydzielonego 0' (w wierszu tym nie ma zera niezależnego 0^*) przechodzi się w kolumnie do zera niezależnego 0^* (o ile takie istnieje), następnie w wierszu do zera wydzielonego i tak naprzemiennie. Można wykazać, że określony w ten sposób łańcuch zer jest wyznaczony jednoznacznie i zaczyna się oraz kończy zerem wydzielonym 0'. W zakończeniu drugiego kroku następuje przemianowanie zer należących do wyznaczonego łańcucha:

0' zmienia się na 0^*

0^* zmienia się na 0

Przemianowana macierz jest macierzą C^k+1. Na tym kończy się k+1 iteracja. Macierz C^k+1 zawiera dokładnie jedno zero niezależne 0^* więcej niż macierz C^k.

Krok 3

Oblicza się minimum z elementów nie wydzielonych:

dla wszystkich par (i,j) indeksów nie wydzielonych.

Następnie tworzona jest macierz
, gdzie:

Wszystkie wyróżnienia macierzy C^k przenosi się na macierz
i przechodzi się do kroku pierwszego. Macierz
zawiera przynajmniej jedno nie wydzielone zero więcej.

Przykład 1

Dany jest problem opisany macierzą C:

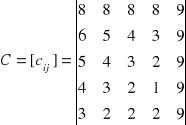
Należy znaleźć rozwiązanie maksymalne metodą węgierską.

Krok przygotowawczy:

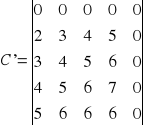
C'=C⁰ (bo w każdym wierszu jest 0, które jest neutralne ze względu na odejmowanie)

Wyznaczenie zer niezależnych:

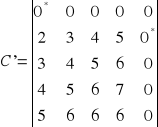
Wyróżnienie kolumn:

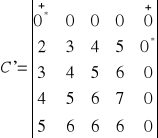
Iteracja 1:

Wydzielenie zer:

Ponieważ wszystkie zera są wydzielone, należy przejść do kroku trzeciego.

Elementy nie wydzielone zaznaczono powyżej. Minimalnym elementem niewydzielonym jest 2 (h =2).

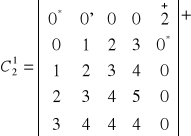
Możliwe do wydzielenia 0 znajduje się w pierwszej kolumnie i w drugim wierszu.

Ponieważ w wierszu tym znajduje się zero niezależne, wydzielony zostaje wiersz, a skasowane wydzielenie kolumny (piątej), w której to zero się znajduje:

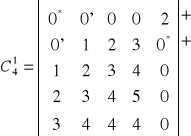
Następne, możliwe do wydzielenia 0 znajduje się w piątej kolumnie i trzecim wierszu:

Ponieważ w wierszu tym nie ma zera niezależnego, tworzony jest łańcuch zer:

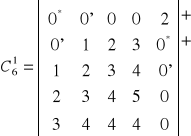
Zakończenie iteracji:

Iteracja 2:

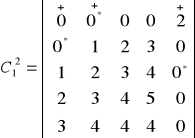
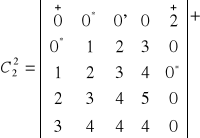
h=1

h=1

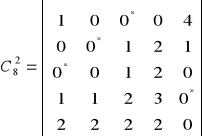
Iteracja 2:

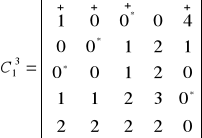
h=1

h=1

Uzyskano pięć zer niezależnych. Ich pozycja wskazuje rozwiązanie maksymalne.

Jeżeli wiersze macierzy C odpowiadają pracownikom, a kolumny czynnościom, to pracownik pierwszy powinien wykonywać czynność 4, pracownik 2 - czynność 2, pracownik 3 - czynność 1, pracownik 4 - czynność 5 i pracownik 5 - czynność 3. Sumaryczny wynik ich pracy wynosiłby 29.

Oprac. Krzysztof Krupa

---