POLITECHNIKA WROCŁAWSKA	Ćwiczenie nr 75
ŁUKASZ STROJWĄS	Wyznaczanie współczynnika załamania za pomocą refraktometru
Wydział Elektroniki Rok I	15.03.2000 OCENA:

1.CEL ĆWICZENIA. Zasadniczym celem ćwiczenia jest poznanie metod wyznaczania współczynnika załamania za pomocą: mikroskopu oraz refraktometru Abbego i Pulfricha.

2.WSTĘP TEORETYCZNY.

Współczynnik załamania
jest jedną z podstawowych wielkości fizycznych służących opisywaniu oddziaływania promieniowania elektromagnetycznego z materią. Jest on związany z przenikalnością elektryczną  i magnetyczną  następującą zależnością:

(*)

gdzie:

c - prędkość fali elektromagnetycznej w próżni;

v - prędkość fazowa fali w danym ośrodku.

Określone w powyższy sposób n nazywa się bezwzględnym współczynnikiem załamania ośrodka. Wielkości n, ,  są zależne od długości fali  promieniowania elektromagnetycznego. Ze wzoru (*) wynika, że:

,

gdzie    - odpowiednio długości fal w próżni i w ośrodku o bezwzględnym współczynniku załamania n.

W czasie t zatem fala biegnąca w próżni przebywa drogę
, a w ośrodku o współczynniku załamania n -

. Z porównania tych dwóch dróg otrzymujemy:

, stąd
.

Ten iloczyn nazywamy drogą optyczną.

Wartość

określa długość odcinka, na którym można odmierzyć tyle samo fal o długości , co na odcinku s. Jeżeli jednej z dwu fal o jednakowych długościach  ustawimy płytę szklaną o grubości d i współczynniku załamania n, to różnica faz obu fal po przejściu przez płytkę wyniesie:

stąd pomiar różnicy faz
lub różnicy dróg optycznych
umożliwia wyznaczenie współczynnika załamania. Fala elektromagnetyczna, przechodząc przez granicę dwóch ośrodków ulega podziałowi na cześć odbitą i załamaną (rysunek poniżej).

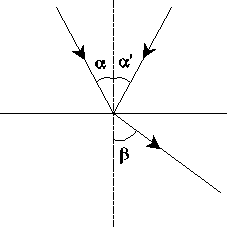
Prawo Snelliusa mówi, że promień padający odbity i załamany oraz prostopadła do granicy rozdziału ośrodków leżą w jednej płaszczyżnie,oraz że między kątami padania  i załamania  istnieje związek:

;

gdzie n - względny współczynnik załamania ośrodka II

Jeżeli światło przechodzi przez granicę ośrodków I i II, gdzie n1>n2, to dla pewnego kąta padania gr kąt załamania =90° i światło nie przechodzi do ośrodka II, czyli:

.

Wzór ten wyrażający związek między kątem granicznym gr i względnym współczynnikiem załamania n, stanowi zasadę pomiaru współczynników załamania za pomocą refraktometru Abbego. Wszystkie promienie padające na powierzchnię graniczną pod kątem większym niż gr , zostają od tej powierzchni całkowicie odbite.

Światło białe, przechodząc przez płaszczyznę rozgraniczającą dwa ośrodki o różnych współczynnikach załamania, ulega rozszczepieniu na poszczególne barwy (długości fal). Zjawisko rozszczepienia nazywamy dyspersją. Przez dyspersję D materiału rozumiemy wielkość:

.

W obszarze dyspersji normalnej współczynnik załamania maleje ze wzrostem długości fali.

3. Przebieg pomiarów.

a) pomiar refraktometrem Abby 'ego:

Zasadniczym celem pomiaru refraktometrem Abby'ego było wyznaczenie współczynnika załamania substancji o różnym procencie stężenia oraz określenie stężenia dwóch substancji na podstawie wyznaczonego współczynnika załamania.

Skalowanie refraktometru.

Po ustawieniu powierzchni polerowanej dolnego pryzmatu w położeniu horyzontalnym, przemyto spirytusem i nałożono kilka kropel wody destylowanej. Układ obu pryzmatów zamknięto mocno zamkiem. Przez obrót układu pryzmatów znaleziono w polu widzenia lunety granice cienia. Na skali lunety odczytano wartość współczynnika załamania cieczy, która wynosiła n=1,333.

Pomiar współczynnika załamania cieczy.

Podobnie jak podczas skalowania, po wyczyszczeniu, naniesiono na pryzmat badaną ciecz. Po uzyskaniu wyraźnej granicy cienia odczytano wartości współczynnika załamania cieczy.

Stężenie[%]	Współczynnik załamania
0	1,333
20	1,377
40	1,426
60	1,463
80	1,499
100	1,544
Substancja X	1,395
Substancja Y	1,443

Na podstawie sporządzonego wykresu możemy z dużym przybliżeniem określić stężęnia substancji X i Y. Stężenie substancji X jest równe około 30%, a stężenie substancji Y około 50%.

b) pomiar za pomocą mikroskopu: W drugiej części ćwiczenia należało dokonaliśmy pomiaru współczynnika załamania szkła za pomocą mikroskopu. W tym celu skorzystaliśmy z wyskalowanej do potrzeb ćwiczenia śruby mikrometrycznej mikroskopu. Wyznaczenia n szkła dokonuje się na gruncie prawa Snelliusa:

.

Korzystając z oznaczeń zamieszczonych na rysunku, możemy zapisać:

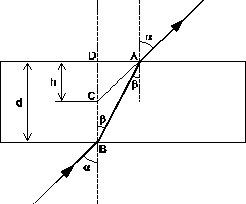
Za pomocą mikroskopu zmierzyć możemy pozorną i rzeczywistą grubość płytki szklanej i na tej podstawie oliczyć n. Dla płytki szklanej otrzymaliśmy następujące wyniki: położenie I 0 - 0 mm

położenie II 60 - 0,6 mmpołożenie III 135 - 1,35 mm.

d=III-I h=III-II

Obliczony współczynnik załamania dla szkła jest postaci:

n=d/h

n=1,35/0,75=1,8

Błąd wyznaczania n dla płytki płytki szklanej wyznaczamy ze wzoru:

h ,, δ,,

Po podstawieniu odpowiednich wartości otrzymujemy:

n1=(1/135+1/75)135/75=0,0373

c) pomiar za pomocą refraktometru Pulfricha:

Za pomocą refraktometru Pulfricha mieliśmy możliwość dokonania pomiaru współczynnika załamania dla wody. Otrzymana wartość współczynnika załamania była postaci:

n=1,33628,

ale po uwzględnieniu poprawki P=0,000156, ostateczny wynik ma postać:

n=1,336436.

4. WNIOSKI I DYSKUSJA WYNIKÓW

Podczas pomiarów refraktometrem Abbego jako błąd n trzeba przyjąć połowę wartości działki elementarnej, czyli: 0.0005. Należy pamiętać, że współczynnik załamania badanej cieczy musi być mniejszy niż współczynnik załamania szkła pryzmatów. Otrzymane za pomocą refraktometru Abby'ego wartości współczynników załamania okazały się dość dokładne, czego dowodem może być chociażby bardzo małe odchylenie zmierzonego współczynnika załamania wody destylowanej od jego wartości zawartej w tablicach n=1,333 (w miejscu tym należy zauważyć, że niewielka różnica pomiędzy wartością odczytaną z tablic, a pomierzoną może wynika choćby z niedoskonałości procesu destylacji wody, który przeprowadzono w miejscowym laboratorium). Poza tym na uwagę zasługuje niska wartość błędu względnego jaki uzyskuje się przy pomiarach refraktrometrem, wyniósł on około 0,03%.

Przy pomiarze współczynnika załamania refraktometrem Pulfricha na uwagę zasługuje możliwość określenia współczynnika z bardzo dużą dokładnością - do szóstej cyfry po przecinku. Fakt ten powoduje, że oceniając oba instrumenty pod względem dokładności, refraktometr Pulfricha gwarantuje bardziej pewny wynik. Wadą refraktometru Pulfricha jest jego sztywna konstrukcja - co utrudniało w penym stopniu możliwość swobodnego przeprowadzania ćwiczenia (nie udało nam się uniknąć konieczności dostosowania wysokości refraktometru do wysokości źródła światła - żółtej linii sodu).

Otrzymane w drugiej części ćwiczenia wyniki jak i obserwacje poczynione w czasie pomiarów współczynnika załamania przy użyciu mikroskopu skłaniają nas do wniosku, że pomiar tą metodą jest obarczony wieloma błędami i nie zapewnia otrzymania bardzo dokładnych wyników.Szczególnie dużo trudności przy tej metodzie sprawia określenie położenia śruby makrometrycznej, przy którym mamy ostry obraz rysy. Rysy wykonane w szkle są zbyt głębokie. W przypadku mikroskopu trzeba pamiętać, że ruch mikro (także makro) służy do ustawienia ostrości mikroskopu, a nie do celów pomiarowych. Podziałka na bębnach śrub nie musi odpowiadać dokładnym wartościom setnych części milimetra.

---