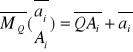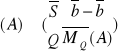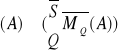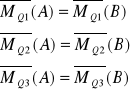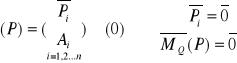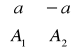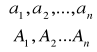Układ tarcz będzie układem tarcz względem siebie niezmiennym geometrycznie jeżeli S=3t-p-2b-3z≤3 jest to warunek tylko konieczny GN. Częściej posługujemy się tzw. Stopniem geometrycznej zmienności V=3t-p-2b-3z-3. o geometrycznej niezmienności decyduje także układ więzów.
WKW geometrycznej niezmienności układu 2 tarcz: V≤0, pręty nie przecinają się w jednym punkcie.
WKW geometrycznej niezmienności układu 3 tarcz: V≤0, punkty przecięć kierunków par prętów między tarczami (przeguby O12,O23 , O31 ) nie mogą leżeć na jednej prostej.
Ortogonalne układy współrzędnych. Ze względów praktycznych jako wektory bazowe przyjmuje się: w przestrzeni D2 dwa wzajemnie prostopadłe wersory e1 i e2 , e=x1 e1 + x2 e2
( c=xc e1 + yc e2 ), c= c1 + c2 = (cx + cy ), w przestrzeni D3 trzy wzajemnie ortogonalne wersowy ei , i=1,2,3 c=c1 + c2 + c3 = x1 e1 + x2 e2 + x3 e3 = xc e1 + yc e2 + zc e3
1.Twierdzenie o równowadze układu sił. WKW równowagi układu sił działających na ciało sztywne jest aby suma tego układu była wektorem zerowym, oraz moment tego układu względem dowolnego bieguna był wektorem zerowym S(A)=0, MQ (A)=0.
2.Twierdzenie o równowadze układu sił. WKW na to aby układ sił na ciało sztywne był w równowadze jest aby momenty tego układu względem 3 nie leżących bna jednej prostej biegunów były wektorami zerowymi MQ1 =0, M Q2 =0, M Q3 =0, Q 1 Q 2 i Q 1 Q 3 nie są do siebie równoległe.
Twierdzenie o trzech siłach. Układ sił jest w równowadze jeżeli siły te leżą w jednej płaszczyźnie, bądź są równoległe, bądź tworzą układ zbieżny o sumie równej 0.
Twierdzenie. W układzie sił wolno którykolwiek wektor przenieść do innego punktu alokacji pod warunkiem dołączenia do układu pary sił o momencie przeniesionego wektora zaczepionego w starym punkcie alokacji a obliczonego względem nowego punktu zaczepienia. 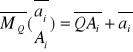
Twierdzenie o redukcji. 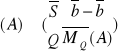
Dowolny układ sił jest równoważny układowi złożonemu z wektora sumy tego układu zaczepionego w dowolnie obranym biegunie, oraz pary sił o momencie układu obliczonym względem tego bieguna. 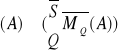
Twierdzenie o równoważności.
1)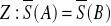
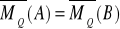
2) 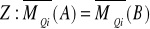
i=1,2,3
Dwa układy są sobie równoważnymi jeżeli ich sumy są sobie równe, oraz ich momenty względem tego samego bieguna są sobie równe.
Dwa układy są sobie równoważnymi jeżeli jest
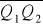
i 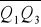
nie są równoległe
1)jeżeli do układu sił działających na CS. Będące w równowadze dodamy lub odejmiemy dwie siły przeciwne leżące na jednej prostej to równowaga ciała nie zostanie naruszona (przekształcenie alfa).
2)jeżeli do układu sił działających na CS będące w równowadze dodamy lub odejmiemy skończony układ sił zbieżnych o sumie równej 0, to równowaga ciała nie zostanie naruszona (przekształcenie beta).
3)jeżeli na ciało sztywne działa zerowy układ sił, to ciało może być w równowadze (lub poruszać się ruchem jednostajnym prostoliniowym).
Osią środkową nazywamy miejsce geometryczne punktów względem których wektor momentu układu jest równoległy do wektora sumy lub równa się zero.
Aby wyznaczyć położenie środka dowolnej liczby sił równoległych należy najpierw wyznaczyć wypadkową. Na prostej działania wypadkowej szukamy punktu niezależnego do wspólnego kierunku wektorów tzn. takiego punktu którego położenie nie zmieni się jeśli wszystkie wektory obrócimy dookoła ich punktu zaczepienia, a ten sam kąt, taki punkt nosi nazwę środka.
Moment statyczny względem statyczny jest równy iloczynowi powierzchni tej figury i odległości jej środka od tej osi.
Wektor siły wypadkowej musi być zaczepiony w odpowiednim punkcie układu tzw. Punkcie zbieżności, natomiast wektor sumy można zaczepiać w dowolnym punkcie układu.
Przestrzenny układ sił można zredukować do skrętnika wtw gdy R=W x MQ≠0, wypadkowej gdy R=0, W≠0, pary sił gdy R=0, W=0, MQ≠0, układowi zerowemu gdy: R=0, W=0, MQ=0.
Wektor główny to wektor sumy układu sił przy redukcji, równowaga układu wystąpi wówczas gdy wektor główny układu jest równy zero.
Przez przekształcenie elementarne α rozumiemy usunięcie lub dołączenie do układu sił (A) układu złożonego z dwóch wektorów przeciwnych leżących na jednej prostej tzn. układu sił.
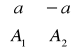
gdzie A1,A2 równolegle do a
Przez przesz kształcenie elementarne β rozumiemy usuniecie lub dołączenie do układu sil(A) układu złożonego z kilku wektorów o wspólnym punkcie zaczepienia i o sumie rownej wektorowi zerowemu tzn. układu sił 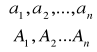
gdzie 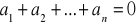
Hodograf wektora- będącego funkcją ciągłą skalara (r=r(t) nazywamy linię ciągłą zakreśloną przez koniec tego wektora gdy jego początek znajduje się w stałym punkcie). Pochodna wektora względem skalara (r=dr/dt) jest wektorem stycznym do hodografu tego wektora w punkcie określonym tym wektorem.
Prędkość średnia. Iloraz 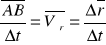
Prędkość chwilowa. Jeżeli istnieje granica ilorazu 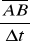
gdy czas 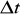
dąży do zera to granicę tę nazywa się prędkością w chwili t.
Chwilowy środek obrotu. W płaszczyźnie kierowniczej znaleźć można taki punkt C, którego prędkość chwilowa jest równa 0 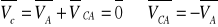
, czyli jest także, 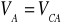
Punkt C nosi nazwę środka chwilowego obrotu.
Energia ruchu obrotowego ciała wynosi, w przybliżeniu małych prędkości oraz modelu bryły sztywnej:

,
W przypadku obrotu wokół jednej z osi głównych wyrażenie na energię kinetyczną w ruchu obrotowym upraszcza się do:

.