IMIĘ I NAZWISKO: Grzegorz Flasiński		LABORATORIUM METROLOGII TECHNICZNEJ
KIERUNEK WM	GRUPA 32A		OCENA	DATA 1999-10-14	PODPIS
TEMAT ĆWICZENIA: „BŁĘDY PRZYPADKOWE W POMIARACH POŚREDNICH”

Cele ćwiczenia:

Celem ćwiczenia było zapoznanie się z błędami przypadkowymi powstałymi w pomiarach pośrednich.

Opis teoretyczny:

Przy wielokrotnych pomiarach tej samej wartości mierzonej wielkości w pozornie niezmienionych warunkach otrzymuje się na ogół różne wyniki pomiarów na skutek występowania błędów przypadkowych. Wyniki te można traktować jako kolejne realizacje zmiennej losowej podlegające regułom statystycznym i stosować przy ich analizie metody rachunku prawdopodobieństwa.

Zmienna losowa x może przyjmować różne wartości (np. wyniki pomiarów) z określonego zbioru liczb, zwanego zbiorem możliwych realizacji tej zmiennej losowej. Rozróżniamy zmienne losowe:

• skokowe (dyskretne): o skończonej lub przeliczalnej liczbie możliwych realizacji;

• ciągłe: gdy zmienna losowa może przyjmować dowolne wartości z określonego przedziału liczb rzeczywistych;

Zdarzeniami losowymi nazywamy zdarzenia polegające na tym, że zmienna x przyjmie określoną wartość x lub wartość z określonego przedziału liczb rzeczywistych. Miarą szans zajścia zdarzenia losowego jest jego prawdopodobieństwo P(A) będące liczbą z przedziału [0,1], przy czym prawdopodobieństwo zdarzenia losowego jest równe 1, a zdarzenia niemożliwego 0.

W celu określenia rozkładu zmiennej losowej skokowej x podaje się zbiór możliwych jej wartości oraz funkcję
określającą prawdopodobieństwo zdarzenia
dla każdej możliwej wartości
danej zmiennej losowej. Funkcja ta nosi nazwę funkcji prawdopodobieństwa zmiennej losowej x.

Na podstawie funkcji prawdopodobieństwa możemy wyznaczyć dystrybuantę (funkcję określającą prawdopodobieństwo tego, że zmienna losowa X przyjmuje wartość mniejszą od x).

Rozkład zmiennej losowej ciągłej określony jest poprzez funkcję gęstości prawdopodobieństwa zmiennej losowej p(x). Jest to granica określona zależnością:

Znaczenie funkcji gęstości prawdopodobieństwa można przedstawić w ten sposób, że jeśli na osi liczbowej ustali się w dowolnym punkcie x dostatecznie małe przedział o dł.
x, wówczas prawdopodobieństwo, że zmienna losowa X o funkcji gęstości p(x) przybierze wartość należącą do tego przedziału, jest w przybliżeniu równa iloczynowi p(x)*
x.

Funkcja gęstości spełnia warunek :

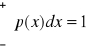
Prawdopodobieństwo, że zmienna losowa X przyjmie wartość z przedziału
wyraża się za pomocą całki:

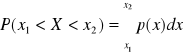
Dystrybuantę zmiennej losowej określa się następująco:

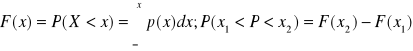
Z rozkładem zmiennej losowej są związane pewne wielkości liczbowe zwane parametrami tego rozkładu. Podstawowym parametrem rozkładu zmiennej losowej X jest jej wartość oczekiwana E(X) nazywana także wartością przeciętną, określająca centrum skupienia wartości tej zmiennej losowej.

Dodatni pierwiastek kwadratowy z wariancji:

Pierwiastek ten nazywany jest odchyleniem standardowym (odchylenie średnie) zmiennej losowej x i stanowi miarę rozrzutu tej zmiennej losowej wokół jej wartości oczekiwanej. W praktyce bardzo często korzysta się z tzw. Standaryzowanej zmiennej losowej, charakteryzującej się tym, że jej wartość oczekiwana jest równa 0, a wariancja jest równa 1.

W analizie błędów największe znaczenie ma rozkład zmiennej losowej zwany rozkładem normalnym (Gaussa). Zmienna losowa ma z reguły rozkład w przybliżeniu normalny, gdy rozrzut jej wartości jest wynikiem sumowania się wpływów wielu różnych przyczyn, z których żadna nie jest dominująca.

Często istnieje potrzeba oszacowania parametrów rozkładu zmiennej losowej w populacji generalnej w sytuacji, gdy musimy ograniczyć się do zbadania próbki losowej z tej populacji. Próbka jest reprezentatywna dla danej populacji, jeśli posiada własności, że rozkład wartości zmiennej losowej w próbce jest zbliżony do rozkładu wartości zmiennej losowej w populacji generalnej. W odniesieniu do wyników pomiarów obarczonych błędami przypadkowymi, najlepszym oszacowaniem wartości oczekiwanej jest wartość średnia.

Na podstawie serii pomiarów traktowanej jako próba losowa z populacji generalnej nieskończonej liczby pomiarów można określić rozrzut pojedynczych wyników pomiaru i średnich arytmetycznych. Miarą tego rozrzutu jest odchylenie średnie kwadratowe średniej arytmetycznej z danej serii pomiarów s
. Ostateczny wynik pojedynczego pomiaru określony jest :

Natomiast wynik serii pomiarów podajemy w postaci:

Na podstawie próby losowej można zbudować histogram, tj. przybliżenie funkcji gęstości. Histogram buduje się w ten sposób, że na osi odciętych zaznacza się przedziały wartości zmiennej losowej i nad każdym przedziałem buduje się prostokąt o polu proporcjonalnym do gęstości prawdopodobieństwa w tym przedziale. Jego wysokość wyraża się zależnością:

m
- liczba wyników pomiaru w przedziale;

d
- długość przedziału;

n- liczba wszystkich pomiarów;

Jeżeli wyniki pomiaru nasuwają wątpliwości, należy to sprawdzić przy pomocy jednego z testów. Jednym z nich jest test chi kwadrat. W celu jego zastosowania należy wyniki pomiarów pogrupować do odpowiednich przedziałów, które obejmują cały zakres zmienności tak, aby ilość wyników pomiarów w poszczególnym przedziale była co najmniej 5. Dla każdego przedziału należy obliczyć prawdopodobieństwo P
, że dany wskaźnik pochodzi z przedziału o wskaźniku 1:

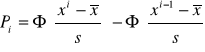
- granice przedziałów;

Następnie należy obliczyć sumę:

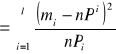
l- liczba wszystkich przedziałów (1
);

n- ilość pomiarów w serii;

m
- liczba wszystkich mieszczących się w i-tym przedziale;

Obliczoną wartość sumy porównujemy z wartością krytyczną przy ustalonym prawdopodobieństwie P i liczbie stopni swobody k= 1 - 3. Jeżeli wartość sumy jest większa od ,to z prawdopodobieństwem P można stwierdzić, że rozkład błędów przypadkowych w rozpatrywanej serii różnie się od rozkładu normalnego. W przeciwnym wypadku brak jest podstaw do takiego stwierdzenia.

Wyniki pomiarów

Wyniki pomiaru wałka I śrubą mikrometryczną :

Tabela

Numer pomiaru	Wynik pomiaru	(xi- )^2
1	14,971	8,0656E-06
2	14,96	6,65856E-05
3	14,971	8,0656E-06
4	14,965	9,9856E-06
5	14,971	8,0656E-06
6	14,968	2,56E-08
7	14,97	3,3856E-06
8	14,968	2,56E-08
9	14,971	8,0656E-06
10	14,97	3,3856E-06
11	14,975	4,67856E-05
12	14,973	2,34256E-05
13	14,971	8,0656E-06
14	14,962	3,79456E-05
15	14,973	2,34256E-05
16	14,963	2,66256E-05
17	14,965	9,9856E-06
18	14,971	8,0656E-06
19	14,962	3,79456E-05
20	14,964	1,73056E-05
21	14,959	8,39056E-05
22	14,96	6,65856E-05
23	14,969	7,056E-07
24	14,971	8,0656E-06
25	14,973	2,34256E-05

Numer pomiaru	Wynik pomiaru	(xi- )^2
26	14,978	9,68256E-05
27	14,976	6,14656E-05
28	14,973	2,34256E-05
29	14,958	0,000103226
30	14,964	1,73056E-05
31	14,968	2,56E-08
32	14,975	4,67856E-05
33	14,976	6,14656E-05
34	14,972	1,47456E-05
35	14,968	2,56E-08
36	14,971	8,0656E-06
37	14,97	3,3856E-06
38	14,968	2,56E-08
39	14,968	2,56E-08
40	14,959	8,39056E-05
41	14,96	6,65856E-05
42	14,962	3,79456E-05
43	14,971	8,0656E-06
44	14,968	2,56E-08
45	14,972	1,47456E-05
46	14,975	4,67856E-05
47	14,971	8,0656E-06
48	14,96	6,65856E-05
49	14,964	1,73056E-05
50	14,965	9,9856E-06

Część obliczeniowa

I. Parametry rozkładów

1. zakres zmienności,

Dla wałka I Dla wałka II

W_min=14,958 W_max=14,978 W_min=38,022 W_max=38,026

b) wartość średnia,

Dla wałka I Dla wałka II

3. błąd średni kwadratowy pojedynczego pomiaru s,

Dla wałka I Dla wałka II

s=0,0052 s= 0,0008

d) błąd średni kwadratowy średniej arytmetycznej s_r ,

Dla wałka I Dla wałka II

s_r=0,0007 s_r=0,0001

e) współczynnik zmienności

Dla wałka I Dla wałka II

k= 0,00035 k=2,2348E-05

2. Ostateczny wynik pojedynczego pomiaru z zadanym prawdopodobieństwem t=2.677.

Dla wałka I Dla wałka II

x=
+t*s=14,9821 x=
+t*s=38,0381

x=
-t*s=14,9542 x=
-t*s=38,0102

III. Ostateczny wynik średniej arytmetycznej z zadanym prawdopodobieństwem t=2.677.

Dla wałka I Dla wałka II

X=
+t*s_r=14,9701 X=
+t*s_r=38,02616

X=
-t*s_r=14,9662 X=
-t*s_r=38,0222

VI. Ostateczny wynik pojedynczego pomiaru i serii pomiarów z błędem maksymalnym t=3.

1. pojedynczego pomiaru

Dla wałka I Dla wałka II

x=
+t*s= 14,9838 x=
+t*s= 38,0398

x=
-t*s= 14,9525 x=
-t*s= 38,0085

2. serii pomiarów

Dla wałka I Dla wałka II

X=
+t*s_r= 14,9704 X=
+t*s_r= 38,0264

X=
-t*s_r= 14,9659 X=
-t*s_r= 38,0212

Tabela pomiarów dla wałka I:

Numer przedziału	Obszar zmienności ­x^i,x^i-1	Częstość mi	Prawdopodobieństwo pi	npi
1	14,956-14,96	7	0,45	3,15	4,70556	29,661
2	14,96-14,964	7	0,9	6,3	0,07778	29,661
3	14,964-14,968	10	0,22	2,2	27,6545	42,3729
4	14,968-14,972	16	0,21	3,36	47,5505	67,7966
5	14,972-14,976	9	0,46	4,14	5,70522	38,1356
6	14,976-14,98	1	-	-	-	-

Tabela pomiarów dla wałka II:

Numer przedziału	Obszar zmienności ­x^i,x^i-1	Częstość mi	Prawdopodobieństwo pi	npi
1	38,022-38,023	10	0,7	7	1,2857	208,333
2	38,023-38,024	22	0,45	9,9	14,7889	458,333
3	38,024-38,025	16	0,45	7,2	10,7556	333,333
4	38,025-38,026	2	-	-	-	-

1

4

---