Zestaw 4

1. Korzystając z definicji granicy ciągu sprawdzić, czy zachodzą równości.

a)
b)
c)

2. Obliczyć granice:

a)
b)
c)

d)
d)
e)

f)
g)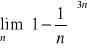
h)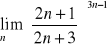

i)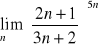
j)

k)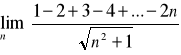

3. Dla podanych szeregów wyznaczyć sumy częściowe S_n i obliczyć sumy szeregów S.

a)
b)
c)

4. Korzystając z kryterium porównawczego lub z warunku koniecznego zbadać zbieżność szeregów:

a)
b)
c)

d)
e)
f)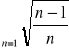

f)
g)

5. Korzystając z kryterium d'Alemberta zbadać zbieżność szeregów:

a)
b)
c)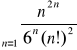

6. Korzystając z wiadomości o szeregach pokazać, że:

a)
b)