1.Cel ćwiczenia
Celem ćwiczenia jest doświadczalne sporządzenie charakterystyki h1=f(Q) koryta mierniczego typu Venturiego o przepływie rwącym oraz wyznaczenie zależności współczynnika przepływu od liczby Froude'a i liczby Reynoldsa.
Tabela pomiarowa
Lp. |
Poziom cieczy h1 [m] |
Czas wypływu T [s] |
Przyrost masy G [kg] |
1 |
0,02 |
10 |
0,055 |
2 |
0,037 |
10 |
0,19 |
3 |
0,050 |
10 |
0,30 |
4 |
0,060 |
10 |
0,40 |
5 |
0,066 |
10 |
0,49 |
b1 = 62 mm = 0,062 m
b2 = 45 mm = 0,045 m
2.Obliczenia:
Ciężar cieczy:
![]()
G=1,479
G=5,11
G=8,07
G=10,76
G=13,18
D - przyrost ciężaru
K - przełożenie dzwigni (wynosi 26,9)
Strumień masowy:
![]()
M=0,147
M=0,511
M=0,807
M=1,076
M=1,318
G - ciężar cieczy
T - czas
Rzeczywiste natężenie przepływu:
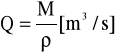
Q=0,000147
Q=0,000511
Q=0,000807
Q=0,001076
Q=0,001318
M - strumień masowy
ρ - gęstość wody ≅ 1000 kg / m3
Teoretyczne natężenie przepływu :
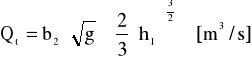
Q=0,000299
Q=0,000752
Q=0,001181
Q=0,001552
Q=0,001791
b2 - szerokość zwężenia koryta
h1 - wysokość cieczy w korycie
g - przyśpieszenie ziemskie
Współczynnik przepływu :
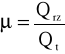
=0,4920
=0,6797
=0,6833
=0,6930
=0,7358
Prędkość przepływu cieczy :
![]()
V=0,1185
V=0,2227
V=0,2603
V=0,2892
V=0,3220
A - pole przekroju przepływającej cieczy. Możemy je wyliczyć ze wzoru:
A = b1 ⋅ h1
A=0,00124
A=0,0022
A=0,0031
A=0,0037
A=0,0040
gdzie:
b1 - szerokość koryta
h1 - wysokość cieczy w korycie
Liczba Reynoldsa :
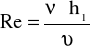
Re=2266,667
Re=4193,333
Re=5666,667
Re=6800
Re=7480
υ - lepkość kinematyczna (wynosi 1,5 *10-6 [ m2/s ])
Liczba Froude'a :
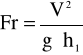
Fr=0,0715
Fr=0,1366
Fr=0,1381
Fr=0,1420
Fr=0,1601
2.Tabele z obliczonymi wartościami:
G |
M |
Qt |
Qrz |
μ |
[ kg ] |
[ kg/s] |
[ m3/s] |
[ m3/s] |
|
1,47 |
0,147 |
0,000299 |
0,000147 |
0,4920 |
5,11 |
0,511 |
0,000752 |
0,000511 |
0,6797 |
8,07 |
0,807 |
0,001181 |
0,000807 |
0,6833 |
10,76 |
1,076 |
0,001552 |
0,001076 |
0,6930 |
13,18 |
1,318 |
0,001791 |
0,001318 |
0,7358 |
Fr |
Re |
A |
V |
|
|
[m2] |
[ m/s] |
0,0715 |
2266,667 |
0,00124 |
0,1185 |
0,1366 |
4193,333 |
0,0022 |
0,2227 |
0,381 |
5666,667 |
0,0031 |
0,2603 |
0,1420 |
6800 |
0,0037 |
0,2892 |
0,1601 |
7480 |
0,0040 |
0,3220 |
3.Obliczanie błędów:
Błąd wyznaczenia liczby Reynoldsa:
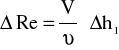
Δh1- błąd odczytu wysokości cieczy, Δh1=0,001 m,
Błąd wyznaczenia liczby Froude'a:
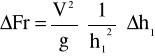
Błąd wyznaczenia prędkości średniej:
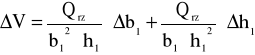
Δb1=0.001[m]
Błąd wyznaczenia rzeczywistego natężenia przepływu:
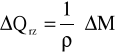
ΔM- błąd rzeczywistej masy przepływu.
Błąd wyznaczenia ciężaru cieczy odczytanej na wadze.
![]()
ΔK=±0,002 - błąd przełożenia dżwigni.
ΔD=±0,005kg - błąd wskazań wagi.
![]()
[kg]
Błąd wyznaczenia rzeczywistej masy przepływu.
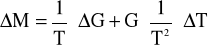
ΔG - błąd ciężaru cieczy.
ΔT - błąd wskazań stopera (wynosi 0,01s)
4.Tabela z wyznaczonymi błędami:
Lp. |
ΔRe |
ΔFr |
ΔV |
ΔM |
ΔQrz |
1 |
79 |
0,003579 |
7,65777E-07 |
0,000416 |
0,000000416 |
2 |
148,4667 |
0,003693 |
4,92986E-06 |
0,00078 |
0,00000078 |
3 |
173,5333 |
0,002763 |
1,05294E-05 |
0,001076 |
0,000001076 |
4 |
192,8 |
0,002368 |
1,68575E-05 |
0,001345 |
0,000001345 |
5 |
214,6667 |
0,002426 |
2,27222E-05 |
0,00165 |
0,000001587 |
5.Wnioski:
Na podstawie wykonanego ćwiczenia można stwierdzić, że rzeczywiste natężenie przepływu wzrasta proporcjonalnie do strumienia cieczy w korycie Venturiego. Współczynnik przepływu wzrasta . Podczas ćwiczenia można było zauważyć, że na zwężeniu koryta w gwałtowny sposób spadała głębokość, po czym za zwężeniem następował ponowny wzrost głębokości. Można było także zaobserwować powstający w niewielkiej odległości za zwężeniem powstający mały odskok Bidone`a. W sposób zauważalny wzrastała prędkość w zwężeniu koryta.
6
Wyszukiwarka
Podobne podstrony:
Przepływ cieczy w korycie Venturiego1
Przepływ cieczy w korycie Venturiego
n19 Przepływ cieczy w korycie Venturiego
Równowaga względna cieczy, Politechnika Opolska
WARUNEK U BORSUKA, Równowaga względna cieczy, Politechnika Opolska
ewa, asi, POLITECHNIKA OPOLSKA
ewa, lab4, Politechnika Opolska
Pomiar natężenia przepływu cieczy roboczej w układach hydrauliki siłowej - sprawko, Uczelnia, Hydrau
Ocena rozw. dzieckaMFDR, Politechnika Opolska - Fizjoterapia
gamma dobree!!, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
przepływ cieczy pod ciśnieniem, BUDOWNICTWO, Inżynierka, semestr 3, Hydraulika i hydrologia, hydraul
NORMALIZACJA, Studia, Maszynoznawstwo (Politechnika Opolska)
fiza ściąga, Politechnika Opolska, 2 semestr, Fizyka - Laboratorium, fizyka Lab, resztki
geologia kolos, Politechnika Opolska Budownictwo, Studia Budownictwo I Sem, Geologia, 0 geologia, 0
Politechnika Opolska
Przepływ cieczy przez duży otwór
wyznaczanie współczynnika strat lokalnych energi przy przepływie cieczyw ukaładach hydraulicznych
Politechnika Opolska
więcej podobnych podstron