68958

intensywniejsze są maksima główne. Oprócz maksimów głównych występują również maksima wtórne. Biorą się one z interferencji promieni z pewnej ilości szczelin i są widoczne w obszaracli minimów oddzielających maksima. Przy dużej liczbie szczelin maksima wtórne niemalże zanikają i pozostają tylko maksima główne.

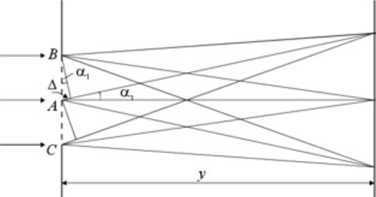
Ćwiczenie polega na wyznaczeniu stałej siatki dyfrakcyjnej tj. odległości między dwiema sąsiednimi szczelinami lub przesłonami. Wielkość tę oznaczamy przez d. Zakładam, że na siatkę pada fala plaska światła monocliromatycznego (warunek ten spełnia w przybliżeniu wiązka równoległa), która po przejściu przez siatkę ulega ugięciu. Ugięte fale pochodzące od sąsiednich szczelin nakładają się i jeżeli spełniony jest warunek dńna^ = kZ, powstaje wzmocniony (jasny) obraz ugiętej fali. Takie zachowanie się światła przedstawiono graficznie na rys. (2)

-i

Rys. 2. Powstawanie prążków dyfrakcyjnych na siatce dyfrakcyjnej

+1

Z rysunku 2 wynika, że różnica dróg A = r/sina, co prowadzi do warunku r/sina* = kZ.

W miejscu oznaczonym O (prążek zerowy) różnica dróg optycznych dla obu promieni wynosi zero. Odpowiada to wartości k = 0 w powyższym w^rzorze. W miejscach oznaczonych +1,-1 wiązki światła tworzą prążki pierwszego rzędu (& = ±1) i analogicznie tworzą się prążki wyższych rzędów. Kąt a* jest kątem, pod jakim z punktuj widać odległość r* pomiędzy prążkiem zerowym a prążkiem ugiętym k-tego rzędu. Przyjmując, że stała d jest niewielka w stosunku do wymiarów x* i y (v oznacza odległość siatki od ekranu), otrzymujemy warunek w^zmocmema obrazu interferencyjnego w postaci:

kZ = d

+ v‘

skąd po przekształceniu otrzymujemy wzór określający stalą siatki dyfrakcyjnej

yR

d = kZ-

+ v

(1)

III. Wykonanie ćwiczenia

W skład układu pomiarowego wehodzi siatka dyfrakcyjna z dodatkowym układem optycznym (szczelina-soczewka) poprawiającym kolimację wiązki. Siatkę dyfrakcyjną oświetla się światłem monoclir oma tycznym.

1 Zestawić układ optyczny wg wskazówek prowadzącego.

2. Włączyć źródło światła.

2