82289

Uwaga 6.16 Jeżeli zamiast nierówności słabych występujących w definicji spełnione są nierówności silne, to ekstrema nazywamy właściwymi.

Przykład 6.13 Korzystając z definicji sprawdzić. czy funkcja ma ekstremum lokalne w punkcie (0,0):

l- y) = 2 - (x² + y¹) 2. f{x, y) = x⁴ - y^Ą

Twierdzenie 6.9 (Warunek konieczny istnienia ekstremum)

Jeżeli funkcja f spełnia warunki:

1.    ma ekstremum lokalne w punkcie Pq.

2.    istnieją pochodne cząstkowe -ff-(Po) ( i = 1____, n),

to (Vi = 1.....n) $(/%) = 0

Przykład 6.14 Sprawdzić, że funkcje: f(x,y) = x² - y². f(x. y) = x³ + y³ spełniają w punkcie (0.0) warunek konieczny, ale nie mają w tym punkcie ekstremum.

Wniosek 6.2 (O lokalizacji ekstremów lokalnych)

Funkcja może mieć ekstrema tylko w punktach, w których wszystkie jej pochodne cząstkowe pierwszego rzędu są równe zew albo w punktach, w których choć jedna z nich nie istnieje.

Uwaga 6.17 Niech funkcja f : A —> 11. A C K² jest klasy C² na A. Wtedy wyznacznik określony następująco:

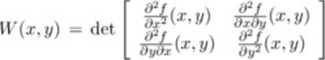
jest funkcją ciągłą. Z twierdzenia o lokalnym zachowaniu znaku wynika, że jeżeli dla pewnego punktu Po(x₀, yo) € intA wyznacznik W{xq, yo) > 0, to istnieje takie otoczenie

O(Po), że

(VP(x,j/)€O(P₀)) W{x,y)> 0

Twierdzenie 6.10 (Warunek wystarczający istnienia ekstremum funkcji dwóch zmiennych)

Niech funkcja f ma ciągle pochodne cząstkowe rzędu drugiego na otoczeniu punktu Po(xo.yo) oraz niech

l- %{x_Q,yo) - 0. ^(*o*J/o) — 0,

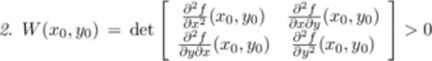
45