82465

Część 2 11. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIL OSIOW YCH 2

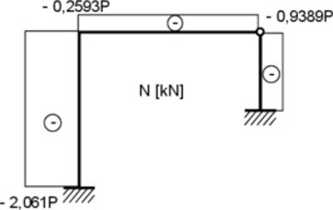
Rys 11.3. Sity wewnętrzne po rozw iązaniu w podejściu klasycznym

Załóżmy teraz, że siła P jest duża i może dojąć do znacznych przemieszczeń. W takiej sytuacji należałoby zapisać równania równowagi w stanie odkształconym, czyli z pomiiuęciem zasady zesztywnierua. Uwzględiueme działania sił normalnych dokonuje się przez rozwiązarue ramy metodą przemieszczeń, z zastosowamem wzorów transformacyjnych w których występują współczynniki a będące funkcją parametru v. Parametr ten jest powiązany z silą nonnalną występującą w pręcie:

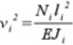
Tak więc postać wzoru transformacyjnego dla poszczególnych prętów' zależeć będzie od wartości siły normalnej. Pojawia się problem, pomewaź chcąc zastosować wzory transformacyjne ze współczynnikami v musimy znać rozkład sił normalnych w ramie statycznie mewyznaczalnej. czyli znać wynik na początku zadania. Poiueważ jest to niemożliwe trzeba najpierw rozwiązać ramę klasycznie i wTznaczyć siły normalne. Dla każdego pręta określić wzoiy transformacyjne z uwzględrueniem wyznaczonych sił normalnych i ponowiue rozwiązać układ.

Otrzymane w^r drugim rozwiązaniu siły będą się różnić od tych. które były podstawą wzorów transformacyjnych (otrzymane z klasycznego rozwiązania). Dlatego obliczenia należy powtórzyć. Taką metodę kolejnych przybliżeń nazywamy metodą iteracyjną. Obliczenia przeprowadza się tak długo, aż wynik nie odbiega znacznie od przyjętego w danym kroku iteracyjnym rozkładu sil (wyznaczonych z poprzedniego kroku).

Dalsze rozważania przeprowadzimy po przyjęciu konkretnej wartości siły P = 30kN. Po pierwszej iteracji otrzymujemy następujące w-artości sił wewnętrznych:

	o r*
o	N[kN] 7/ 77	o

- 61.835

Rys. 11.4. Sity wewnętrzne po iteracji I (rozwiązanie metodą klasyczną)

AlmeiMater

Dobra D.. Dzlakirwlcz L.. Jainbroźrk S., kanma M.. Mikołajczak K.. Przybylska P., Sytak A.. Wdowdca A