CCF20120509112

.ino częsc 11. itozwiązama i uupuwieu/.i

Jeżeli uwzględnimy czas zamknięcia zaworu t_z i czas przejścia fali uderzeniowej t, wzór na przerost ciśnienia wywołanego uderzeniem hydraulicznym będzie miał następującą postać:

A p = — pu(c — c₀) — .    (12)

6.1. Jednowymiarowy nieustalony przepływ cieczy

6.1.1. W równaniu bilansu energii dla przekrojów 1 i 2 (rys. 11-6.4)

fi ,Pi

20 y

+ ^zi

S2

iJ

^• + — + z₂ + - I ^ds,

20    y 0 J 3t

0C

mamy:

^C1 ^{— C}2 ^{— C}> Pl ~ Pl ~ Pb’ z_v = z, z₂ = o, z + X = H,

S2

Jds = z + jc = H,

Si

3c    dc    d²z

31    dt    dr² ’

HcPz

z =

7d?’

czyli

cPz.

dr

■ +

i¹-⁰-

Wprowadzając

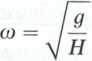
otrzymujemy równanie drgań mechanicznych nietłumionych

d ²z

-_Ty + co^zz = 0, dr

którego ogólne rozwiązanie możemy przedstawić w następującej postaci:

z = Cjsincof + C₂coscot.

Z warunków brzegowych:

otrzymamy:

dla t = 0, C, = 0 oraz

z = H, C₂ = H,

a zatem

z = H cos wt.

Z ostatniego wyrażenia wynika, że poziom cieczy obniża się w czasie według równania cosinusoidy.

W chwili opróżnienia rury pionowej z = 0, czyli

cos wt = 0,

wobec tego

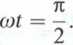
W związku z tym, czas opróżniania

t

n

2co ’ a po podstawieniu

K

2

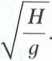
t