CCF20120509077

LVtL ^zęsc 11. Kozwisgzama i uupowieuzi

Dla

4nv„

r = 0 oraz z.

otrzymamy

r² Q z

V„—~

Q

Jeżeli z->oo, to

2    4 7t y_r² + z² 4n

1, przeto promień opływanej bryły obrotowej

=

Q

nv„

e. Z równania Bernoulliego dla płynu doskonałego

P ^_Poo , ^VA P 2 p 2’

po uwzględnieniu wyrażenia (5), wyznaczymy pole ciśnienia

P ^{= P}°>-2

^v°°Q^zJoy¹

2nR³ \4n R*

4.4.5. Do funkcji

w (z) = (p(x,y) + i\l/{x,y) = v₀₀\z+— ,

wprowadzamy postać wykładniczą zmiennej zespolonej:

z = r e^l9 = r (cos 9 + i sin 9),

skąd po przyrównaniu części rzeczywistych i urojonych otrzymamy:

ę = tf^l +^jrcos9,

<A = vJl~jrsin9.

Ponieważ

z = x + iy,

czyli

x - rcos9, y = rsin 9,

gdzie

r² = x² + y²,

zatem potencjał prędkości oraz funkcję prądu możemy zapisać w postaci:

<P = v a

x² + y² + l3 ’ x² + y² '

(3)

oraz

(4)

(5)

(6)

x² + y² — L²

Kównanie rodziny linii prądu (t/r = C/a^) wyrazimy następująco:

L²\ . „ C

r--sin .V = —

r /    a^

lub

I )la zerowej linii prądu

wobec tego

oraz

(x² + y²-L²)y = C_l(x² + y²).

C = C_t = 0,

r² = L², sin ,9 = 0 x² + y² = L², y = 0.

Z powyższego wynika, że zerową linią prądu jest okrąg o promieniu L, którego rodek znajduje się w początku układu osi współrzędnych. W związku z tym, dializowany przepływ można uważać za opływ walca o promieniu równym L (rys. II 4.16).

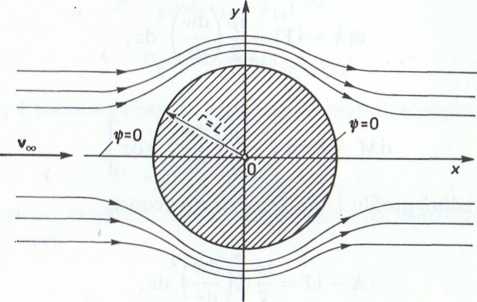
Rys^-łTą. 16